Производная по направлению и градиент.

Если функция F дифференцируема в точке Х, то она имеет в этой точке производную по любому направлению l.

Определение 1. Производной функции F(X) по направлению l в точке Х⁰ называется предел 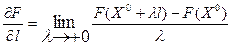. (8.4)

Направление l обычно задается вектором l = (l₁, l₂, …, l_n).

Производная функции F по направлению l выражается через частные производные этой функции по формуле

(8.5)

где l_i – длина проекции вектора l на ось х_i;

|l| - длина вектора l, т.е. .

Абсолютная величина производной функции по направлению l дает скорость изменения функции в этом направлении, а знак показывает характер изменения функции (возрастание или убывание).

Определение 2. Градиентом 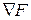функции F(X) называется вектор, проекциями которого на координатные оси служат соответствующие частные производные этой функции, т.е.

=

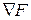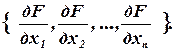
Можно показать, что max достигается тогда, когда направление l совпадает с направлением 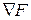. По формуле (8.5) производная функции F по направлению 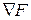равна

Таким образом, в каждой точке Х направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.

Выпуклые функции обладают следующими аналитическими и алгебраическими свойствами:

1. Если функция F(X) выпукла, то функция –F(X) вогнута.

2. Выпуклая (вогнутая) функция, определенная на выпуклом множестве М, непрерывна в каждой внутренней точке этого множества.

3. Если функции выпуклые при всех неотрицательных значениях переменных, то область решений системы неравенств является выпуклым множеством (если она не пуста).

4. Всякая дифференцируемаястрого выпуклая (вогнутая) функция имеет не более одной стационарной точки (т.е. точки, в которой равны нулю все частные производные). При этом для выпуклой (вогнутой) функции стационарная точка всегда является точкой локального и глобального минимума (максимума).

5. Дважды дифференцируемая функция F(X) является выпуклой в том и только в том случае, когда

(8.6)

для любых Х М и Δx_i, Δx_j, не обращающихся в нуль одновременно.

Дата добавления: 2015-09-01