Производная в демографии.

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t), . Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Выполним ряд простейший преобразований и выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.

Опираясь на данную модель знаменитого демографа, попробуем выяснить возможность применения производной в этой сфере.

Пусть у = у(t) - численность населения.

Рассмотрим прирост населения за Dt = t-t₀

Dy = k y Dt, где k = k_р – k_с –коэффициент прироста (k_р – коэффициент рождаемости,

k_с – коэффициент смертности)

=k y

При Dt® 0 получим = y

у = к у

Вследствие, проведенных нами преобразований можно сделать вывод, что и здесь производная широко применима и дает устойчивую систему решений определенных вопросов в этой сфере.

Производная в экономике.

В особенности применение производной востребовано в экономике.

Давайте рассмотрим применение производной к решению следующей экономической задачи:

Р - ежегодное потребление продукта на душу занятых в производстве;

x - число занятых в производстве рабочих.

Величины Р и x связаны следующей функциональной зависимостью

, M,b - постоянные, характеризующие производственные возможности хозяйства.

При M=250,b=8464 определить число рабочих, соответствующее наибольшему значению Р в хозяйствах с 80,90,120 и 150 рабочими местами.

Решение

(раскроем скобки и представим дробь в виде разности трёх переменных).

Исследуем функцию на наибольшее значение при х >0. Для этого найдём производную и прировняем её к нулю:

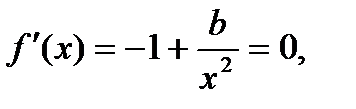
Так как х >0, то .

х

+

f ’

-

f

Исследуя знак производной, легко убедиться в том, что функция монотонно возрастает, а при х >92- монотонно убывает .

Следовательно, на отрезке от 1 до 80 функция возрастает, и её наибольшее значение достигается на правом конце х=80.

А на отрезках от 1 до 120 и от 1до 150 функция меняет характер монотонности, отсюда следует, что наибольшее значение достигает в точке

х = 92.

Производная помогла определить, что хозяйству нет смысла набирать 120 и 150 человек для достижения наибольшей прибыли.

2. П (t) = υ (t) - производительность труда,

где υ (t) - объем продукции

J(x) = y (x) - предельные издержки производства,

где y– издержки производства в зависимости от объема выпускаемой продукции x.

2.Оборот производительности труда за истекший год описывается через функцию U(t)=0,15t³ – 2t² + 200, где t – месяцы,U -денежные единицы

Исследуйте оборот предприятия за 9 и 10 месяцы.

Решение. Исследуем оборот предприятия с помощью производной: U'(t)=0,45t² - 4t

V(t)=U (t)

Подставим t:

V()=0.45

V()=0.45

V()<v()

Сравнивая показатели, обнаружим что оборот производительности труда предприятия на 9 месяце был значительно меньше, чем на 10.

3. Функция спроса имеет вид Q_D=100 – 20p, постоянные издержки TFC (total fixed costs) составляют 50 денежных единиц, а переменные издержки TVC (total variable costs) на производство единицы продукции – 2 денежные единицы. Найти объём выпуска, максимизирующий прибыль монополиста.

Решение: Прибыль есть выручка(TR) минус издержки (TC):

П=TR – TC,

где TR= p*Q (p-цена товара,Q-количество товара);

TC=TFC+TVC (TFC-фиксированные издержки,TVC-переменные издержки)

Найдём цену единицы продукции:

20p=100 – Q p=5 – Q/20.

Тогда

П=(5 – Q/20)Q – (50 + 2Q)= – Q² + 60Q - 1000

Найдём производную: П'(Q)= –2Q+60.

Приравняем производную к нулю: –2Q+60=0 Q=30.

При переходе через точку Q=30 функция П(Q) меняет свой знак с плюса на минус, следовательно, эта точка является точкой максимума, и в ней функция прибыли достигает своего максимального значения. Таким образом, объём выпуска, максимизирующий прибыль, равен 30 единицам продукции.

Дата добавления: 2015-09-05