Замечание. Обращаем внимание на то, что в данной теореме доказана монотонность функции f(x)в

Обращаем внимание на то, что в данной теореме доказана монотонность функции f(x) в некотором промежутке [ a,b ] в предположении f (x)≥0(>0) или f (x)≤0(<0) внутри всего этого промежутка. Если же известно,что f 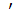( )>0(<0) в одной точке ,то отсюда нельзя заключить, что f(x) монотонна хотя бы в малой окрестности точки .в качестве примера рассмотрим функцию:

F(x)= .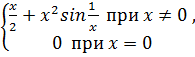

Ее производная f’(x)= 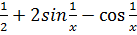.значение f '(0) из этой формулы получить нельзя, так как при x=0 выражение 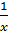теряет смысл. Найдем

f (0),исходя из определения производной:

.

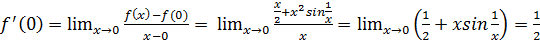Покажем, что хотя f 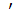(x)>0,тем не менее, ни в какой окрестности нуля функция не монотонна. Действительно, если взять точки, то если же взять точки:

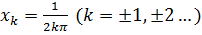,то, f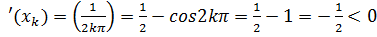

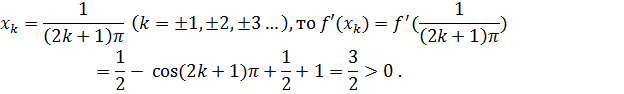
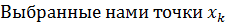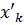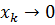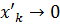и попадают в любую окрестность нуля т.к и при 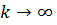.следовательно, производная функции меняет знак в любой окрестности нуля, что и доказывает наше утверждение. Этот факт имеет место, очевидно, из-за того, что производная f (x) в нуле имеет разрыв.

Дата добавления: 2015-09-05