
Читайте также:
|
1. Пусть, 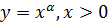 найдем
найдем 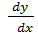 . Имеем
. Имеем 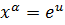 ,где
,где 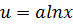 .
.
Заметим, что 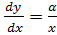 , получаем
, получаем 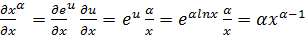 .
.
Следовательно, 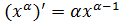 .
.
Например,
если, y= 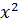 то
то 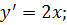
если, 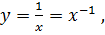 то
то 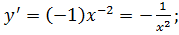
если, 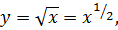 то
то 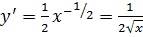
Если функция y= 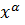 определена при x<0,то при этих значениях x она также имеет производную y
определена при x<0,то при этих значениях x она также имеет производную y  =
= 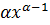 .
.
2.Пусть y=ln|x|, 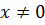 ;тогда при x >0 имеем,
;тогда при x >0 имеем,
а при x<0
y  = [ln(-x)]’=
= [ln(-x)]’= 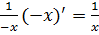 .
.
Таким образом, для всех 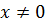 справедлива формула
справедлива формула
(ln|x|)  =
= 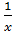 (5.3)
(5.3)
Отсюда, по правилу дифференцирования сложной функции, для любой функции u(x) в точках x,в которых существует производная u  (x),а u(x)≠ 0 имеет место соотношение:
(x),а u(x)≠ 0 имеет место соотношение:
(ln|u(x)|) 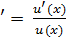 (5.4)
(5.4)
3.Найдем производную функции
y= 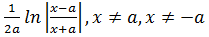 . В силу имеем
. В силу имеем
y’= 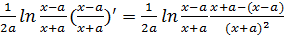 =
= 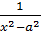
Замечание. Используя теорему 4,можно все полученные формулы для производных основных элементарных функции записать в более общем виде: если u=u(x) –дифференцируемая функция, то:
· (sin u)  =u
=u  cosu;
cosu;
· (cos u)  =- u’sinu;
=- u’sinu;
· (tg u)  =
= 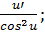
· (ctg u)  =-
=- 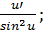
· 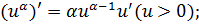
· 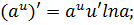
· 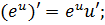
· (ln u)  =
= 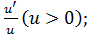
· (arcsin u)  =
= 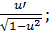
· (arcos u)  = -
= - 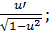
· (arctg u)  =
= 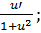
· (arcctg u)  =
= 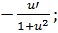
Из приведенных формул видно (при x=u),что производные основных элементарных функций являются элементарными функциями.
Полученные же в совокупности формулы дают возможность вычислить производную и дифференциал любой элементарной функции в случае, если эта производная существует.
Следует иметь в виду, однако, что не всякая элементарная функция имеет производные во всех точках своей области определения.
примером элементарной, дифференцируемой не во всех точках функции является функция | x |= 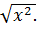 Она, как мы знаем, не имеет производной в точке x=0.
Она, как мы знаем, не имеет производной в точке x=0.
Дата добавления: 2015-09-05; просмотров: 65 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема 5.1. | | | Доказательство |