Доказательство. Пусть для определенности f(x ) принимает в точке c наибольшее значение

Пусть для определенности f(x) принимает в точке c наибольшее значение, так что для всех x из X:

f(x)≤ f(c)

По определению производной:

f (c) ,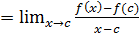

причем предел этот не зависит от того, будет ли x приближаться к c справа или слева.

Но при x >c выражение примет вид:

,

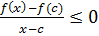так что и в пределе, при 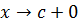, получится:

f (c)≤ 0 (1)

Если же x < c, то ,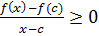

и переходя здесь к пределу при 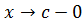, найдем:

f (c) ≥ 0 (2)

Сопоставляя соотношения (1) и (2),приходим к требуемому заключению:

f (c)=0.

Дата добавления: 2015-09-05