Примеры. 1.Пусть ; в силу формул 4.1,4.2 и 4.4 имеем

1. Пусть 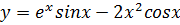; в силу формул 4.1,4.2 и 4.4 имеем

y = ( 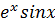) - 2( ) = .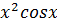

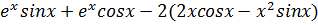2. Пусть 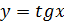; так как 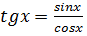, то по формуле (4.3)получаем

.

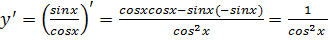Таким образом, .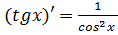

3. Аналогично, для y=ctg x

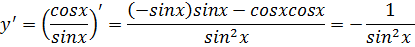
т.е. (ctg x) = .

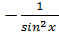Свойства(4.1-4.4) переносятся и на дифференциалы функций.

При тех же предположениях относительно дифференцируемости в точке имеем:

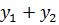d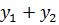( )=d d( )= ,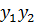

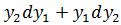d(cy) =cdy, d( =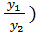

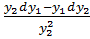
Вычислим, например, дифференциал произведения y = :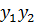

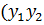dy = y dx= ) dx=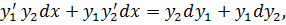

так как .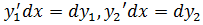

Аналогично доказываются остальные формулы.

Дата добавления: 2015-09-05