
|
Читайте также: |
Используя свойства бесконечных пределов, относящиеся к арифметическим действиям над функциями, можно установить и соответствующие свойства бесконечных производных. Например, если существует конечная производная 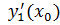 и бесконечная (определенного знака) производная
и бесконечная (определенного знака) производная 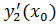 ,то у функции y(x)=
,то у функции y(x)= 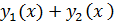 в точке
в точке 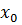 существует бесконечная производная того же знака.
существует бесконечная производная того же знака.
Например, если 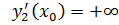 , то
, то 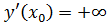 . Действительно, ∆ y=∆
. Действительно, ∆ y=∆ 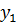 +
+ 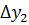 .Поэтому, если существует конечный предел
.Поэтому, если существует конечный предел
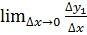 , а
, а 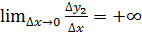 ,
,
то 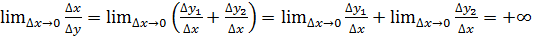 т.е.
т.е. 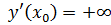 .
.
Дата добавления: 2015-09-05; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Правила вычисления производной. | | | Примеры |