Односторонние производные.

Если для некоторого значения x ₀ существует один из пределов: 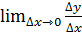=∞, = 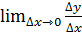+∞ или 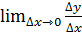= -∞, то говорят, что при 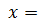x ₀ существует бесконечная производная или соответственно бесконечная производная определенного знака, равная +∞ или -∞.

Определение 3.1.

Если функция 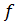определена в некоторой правосторонней (левосторонней) окрестности точки x₀ и существует конечный или бесконечный предел:

( ),

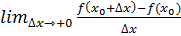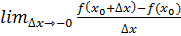то он называется соответственно конечной или бесконечной правой (левой) производной функции 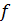в точке 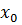и обозначается 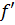₊ (x₀) (или 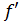_- (x₀)).

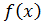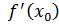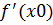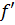Из теоремы об односторонних пределах (см.5.9 в [1]) следует, что функция , определенная в некоторой окрестности точки x ₀,имеет производную тогда и только тогда, когда ₊(x ₀) и _-(x ₀) существуют и ₊(x ₀) = _-(x ₀). В этом случае = ₊(x ₀) = 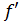_-(x ₀).

Пример

Функция f(x)= 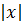очевидно, непрерывна в точке x=0, но не имеет в этой точке производной.

В самом деле, при имеем , поэтому для точки

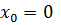получим .

Следовательно, .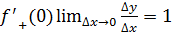

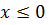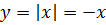Аналогично, при имеем , поэтому для точки 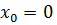в этом случае получим .

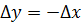Следовательно,

.

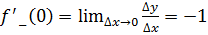Тем самым доказано, что функция f(x)= 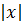не имеет при x=0 производной, однако в этой точке существуют как левая, так и правая производные.

Отметим ещё, что при x >0 имеет место равенство (, а при x<0 соответственно 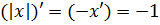, поэтому для любого x ≠ 0 справедлива формула .

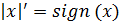Дата добавления: 2015-09-05