Теорема 5.1.

Пусть функция y = f(x) имеет производную в точке , а функция z = F(y) имеет производную в точке ).тогда сложная функция Ф(x)=F[f(x)] также имеет производную при x = ,причем

Ф'(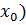 =F ( (5.1)

Доказательство (с.294.[1])

Если сложную функцию Ф обозначить символом Ф=F (см.п.5.2 [1]), то формулу (5.1)можно записать в виде:

(F .

Следует обратить внимание на то, что утверждение о существовании в точке 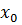производной сложной функции F[f(x)] содержит предположение о том, что рассматриваемая сложная функция имеет смысл, т.е. определена в некоторой окрестности точки .

Опуская значение аргумента, и используя запись производной, с помощью дифференциалов равенство можно переписать в виде

= .

Следствие (инвариантность формы первого дифференциала относительно преобразования независимой переменной):

dz = F ( )dy=Ф ( )dx. (5.2)

В этой формуле 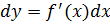является дифференциалом функции у (х),

а dx -дифференциалом независимой переменной.

Таким образом, дифференциал функции имеет один и тот же вид: произведение производной по некоторой переменной на «дифференциал этой переменной» - независимо от того, является эта переменная, в свою очередь, функцией или независимой переменной.

Доказательство. Согласно формуле (5.2) dz= Ф’( )dx, Отсюда, применив формулу (5.1) для производной сложной функции, получим dz= F ( ,но ,поэтому dz= F ( .

Формулу (5.1) можно интерпретировать и несколько иначе, если вспомнить, что дифференциалом функции в точке является функция, линейная относительно дифференциала независимой переменной. Согласно (5.1), дифференциал функции Ф(x)=F(f(x)) имеет вид dФ=F'(y)f ) dx. То есть является результатом подстановки линейной функции ,с помощью которой задан дифференциал, df (где y=f(x)) в линейную функцию dz= , задающую дифференциал dF (где z=F(y)). иначе говоря, дифференциал композиции Ф является композицией дифференциалов, dF и df:

Отметим, что теорема 5 по индукции распространяется на суперпозицию любого конечного числа функций. Например, для сложной функции вида z(y(x(y))) в случае дифференцируемости функций z(y), y(x) и x(t) в соответствующих точках имеет место формула

= .

Дата добавления: 2015-09-05