Определение 3.1.

Функция 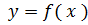, определенная в некоторой окрестности 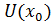точки x₀ ∊ R, называется дифференцируемой при 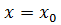,если ее приращение в этой точке, т.е. 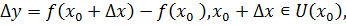представимо в виде

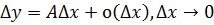, (1.2)

где –A постоянная.

Заметим что дифференциал 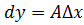, как и всякая линейная функция, определен для любого значения :

-∞ ∞,

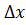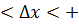в то время как приращение, 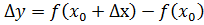естественно, можно рассматривать только для таких 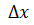, для которых 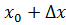принадлежит области определения функции f.

Если A≠0, т. е если dy 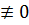,то дифференцируемость функции в точке x ₀ означает, что с точностью до бесконечно малых более высокого порядка, чем приращение аргумента 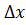, приращение функции 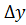является линейной функцией от .

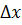Если же A= 0, т. е dy 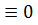, то ∆y = о(∆x) при 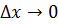. Таким образом,

при A = 0 приращение 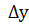является бесконечно малой более высокого порядка, чем 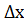, когда .

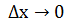Для большей симметрии записи дифференциала приращение обозначают dx и называют его дифференциалом независимого переменного. Таким образом,дифференциал можно записать в виде dy =Adx.

Пример ы:

Найдем дифференциал функции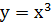

Решение:

В этом случае,

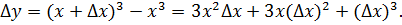
При 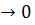главная линейная часть выражения, стоящего справа, равна 3 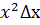; поэтому dy=3 .

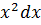Пусть f( )= . Подставив в (1.2) значения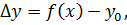

t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>0</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 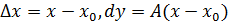,получим

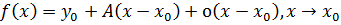
Итак, если функция f(x) дифференцируема в точке , то с точностью до бесконечно малых более высокого порядка, чем x- 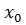вблизи 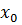она равна линейной функции; иначе говоря, в этом случае функция f в окрестности точки 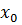ведет себя «почти как линейная функция» 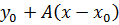,причем погрешность при замене функции f этой линейной функции тем меньше, чем меньше разность 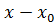,и,более того, отношение этой погрешности к разности 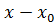,т.е. относительная погрешность, стремится к нулю при .

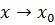Если функция f дифференцируема в каждой точке некоторого интервала, то ее дифференциал является функцией двух переменных - точки и переменной dx:

.

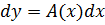Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке.

Теорема 3.1.

Для того чтобы функция f была дифференцируемой в некоторой точке 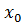, необходимо и достаточно, чтобы она имела в этой точке производную;

при этом:

dy =f ( ) dx.

Дата добавления: 2015-09-05