Аналитическое определение эффективности и гидравлического сопротивления пористого фильтра

При определении эффективности пористых фильтров основным параметром является суммарный коэффициент захвата частиц пыли элементом фильтрующего слоя. Следует иметь в виду, что нельзя непосредственно определять по формулам, приведенным выше. Дело в том, что фильтрующий слой представляет собой совокупность фильтрующих элементов, близко и беспорядочно расположенных по отношению друг к другу. Вследствие этого поле скоростей в реальном, даже изотропном фильтре сильно отличается от поля скоростей вокруг изолированных фильтрующих элементов (цилиндра, шара). Эффективность отдельных фильтрующих элементов, расположенных внутри фильтрующего слоя, может быть больше или меньше той, которая наблюдается для тех же элементов, расположенных изолированно. Для определения суммарных коэффициентов захвата фильтров различного вида предложено много формул, основанных на различных, главным образом полуэмпирических теориях, которые будут приведены ниже при рассмотрении пористых фильтров различного типа.

В общем виде степень очистки можно определить исходя из следующих рассуждений.

Количество фильтрующих элементов N в единице объема фильтрующего слоя толщиной Н равно

N = αH/V₁, (5.18)

где α — плотность упаковки слоя; V ₁— объем одного фильтрующего элемента.

Количество частиц, уловленных каждым фильтрующим элементом, может быть найдено из выражения

, (5.19)

где — суммарный коэффициент захвата фильтрующего элемента в условиях фильтрующего слоя; F ₁— площадь сечения фильтрующего элемента, нормального к направлению движения потока; w' — действительная скорость газа в порах между фильтрующими элементами; w ' = w _ф/(1—α); z - —количество частиц, содержащихся в единице объема газа (счетная концентрация), перед пористой перегородкой.

Математически процесс фильтрации может быть описан следующим дифференциальным уравнением, выражающим материальный баланс частиц пыли при прохождении через единицу площади пористой перегородки толщиной dH:

. (5.20)

Физический смысл этого уравнения сводится к тому, что убыль частиц в потоке газа, проходящем через фильтрующий слой, равна суммарному количеству частиц, уловленному всеми фильтрующими элементами этого слоя.

После разделения переменных и интегрирования в пределах от z₀ до z и от 0 до H получим

и 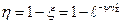(5.21)

Величина ψ получила название показателя структуры фильтрующего слоя, так как она зависит от плотности упаковки а и геометрических характеристик слоя:

. (5.22)

Очевидно, что аналитически эта величина может быть определена только для тел простейшей формы (шара, цилиндра).

Любые пористые фильтры, как правило, многослойны (фильтрующие слои работают последовательно). Масса пыли, осажденная на всем фильтре, равна сумме масс, уловленных каждым из слоев. Если считать, что степень очистки для всех слоев одинакова, то степень проскока каждого слоя равна

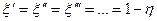. (5.23)

При п слоях общая степень проскока x_о и степень очистки h _о многослойного фильтра будут соответственно равны

; (5.24)

. (5.25)

Полученные выражения являются приближенными, так как ими не учитываются струйный характер поступления газа из слоя в слой, турбулизация газового потока в фильтре и изменение фракционного состава пыли от слоя к слою. Тем не менее, они дают возможность по пылезадерживающей способности одного слоя прогнозировать предполагаемую эффективность многослойного фильтра.

Как показывают теоретические и экспериментальные исследования, в пористых фильтрах в подавляющем большинстве случаев режим движения газа ламинарный. Лишь в зернистых фильтрах при высоких скоростях фильтрования можно наблюдать режимы движения, находящиеся в переходной области. Вследствие этого для определения гидравлического сопротивления пористых перегородок широко используют закон Пуазейля:

. (5.26)

Эквивалентный радиус поровых каналов может быть выражен через радиус фильтрующих элементов r_экв = δr₀.

Суммарную эквивалентную длину порового канала l_Σ выражают обычно через толщину слоя Н, т. е. l_Σ=a²H, где а — коэффициент извилистости пор, учитывающий, с одной стороны, увеличение длины канала по сравнению с толщиной слоя, а с другой — эквивалентную длину местных сопротивлений порового канала.

Фактическую скорость газа в канале w' выражают, как обычно, через скорость фильтрования

w'=w_ф/(1—а). (5.27)

После подстановки указанных величин в уравнение (5.26) последнее примет следующий вид:

, (5.28)

где К_о — коэффициент сопротивления пористой среды;

К_о= 8а/(1-α)δ. (5.29)

Для определения этой величины ниже будет приведен ряд формул полуэмпирического вида в соответствии с характером пористой перегородки, т. е. типом фильтра. В общем случае пористую перегородку можно представить состоящей из двух слоев: первичный — сама пористая перегородка с осажденными на стенках поровых каналов частицами пыли, вторичный — слой уловленных частиц, накапливающихся на лобовой поверхности фильтра.

С течением времени сопротивление первичного слоя изменяется вследствие постоянного уменьшения его пористости, а вторичного в результате постепенного его утолщения. Таким образом, общую потерю давления на фильтре D р можно представить как сумму потерь давления в каждом из слоев:

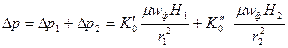. (5.30)

Потеря давления в первичном слое фильтра D р ₁ может быть определена по формуле

D р ₁= Аmw _ф. (5.31)

где А — коэффициент, зависящий от пористости, геометрических и аэродинамических характеристик слоя; A = f(K₀´HM_o), здесь М_о — пылеемкость первичного слоя фильтра.

Потеря давления в образующемся лобовом слое пыли Dр₂ может быть подсчитана из выражения

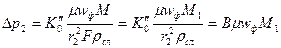, (5.32)

где М, M ₁— масса пыли, оседающей соответственно на всей площади фильтра и на 1 м² площади его, кг; r_сл — плотность пылевого слоя, кг/м³; В — коэффициент, зависящий от пористости, геометрических и аэродинамических характеристик образующегося вторичного слоя пыли; .

Следовательно, общая потеря давления на фильтре равна

D p=mw _ф(А+ВМ ₁).(5.33)

Вследствие того что степень очистки в пористых фильтрах в рабочем состоянии близка к 100%, величину M ₁приближенно можно определить по начальной концентрации пыли в газовом потоке:

М₁ = z ₁ w_фt, (5.34)

где t — время, отсчитанное от начала эксплуатации фильтра, с

Численные значения коэффициентов А и В определяются опытным путем.

Контрольные вопросы

1. Физические основы процесса фильтрования.

2. Механизмы процесса фильтрования.

3. Как составить дифференциальное уравнение, описывающее процесс очистки запыленного газа в фильтре?

4. От каких факторов зависит эффективность пористого фильтра?

5. Как определяют гидравлическое сопротивление пористого фильтра?

Дата добавления: 2015-09-02