Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Доказательство необходимости

Ф.Энгельс | Определение 1.1 | Односторонние производные. | Доказательство | Правила вычисления производной. | Замечание | Примеры | Теорема 5.1. | Примеры | Доказательство |


Читайте также:
  1. Времени достаточно, не торопите себя без необходимости, но и не теряйте его понапрасну!
  2. Доказательства необходимости искупления
  3. Доказательство
  4. Доказательство
  5. Доказательство
  6. Доказательство
  7. Доказательство достаточности

Пусть функция f дифференцируема в точке , т.е .

Тогда

s w:val="28"/></w:rPr><m:t>=A.</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="00617C7A"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

Поэтому производная f ( ) существует и равна A.отсюда

dy =f 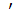( )dx.

Дата добавления: 2015-09-05; просмотров: 44 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Определение 3.1.| Доказательство достаточности
mybiblioteka.su - 2015-2025 год. (0.005 сек.)