
Читайте также:
|
Получим теперь формулы для производных суммы, произведения и частного функции.
Теорема 4.1.
Пусть 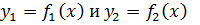 функция и определены в окрестности точки
функция и определены в окрестности точки 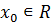 и имеют в самой точке
и имеют в самой точке 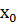 производные, тогда и их сумма
производные, тогда и их сумма 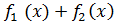 произведение
произведение 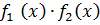 , а если
, а если 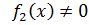 , то и частное
, то и частное 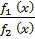 имеют в точке
имеют в точке 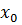 производные, причем:
производные, причем:
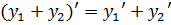 (4.1)
(4.1)
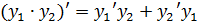 (4.2)
(4.2)
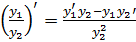 (4.3)
(4.3)
(в формулах 4.1- 4.3, при x=  )
)
Следствие 1. Если функция y=f(x) имеет производную в точке 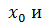 c ∊ R,то функция также имеет в этой точке производную, причем:
c ∊ R,то функция также имеет в этой точке производную, причем:
(c y)  =cy
=cy  (x= r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
(x= r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 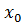 ) (4.4)
) (4.4)
Следствие 2. Если функции  , k=1,2…,n, имеют в точке
, k=1,2…,n, имеют в точке 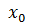 производные, то всякая их линейная комбинация также имеет в этой точке производную, причем
производные, то всякая их линейная комбинация также имеет в этой точке производную, причем
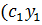 +….+
+….+  )
)  =
= 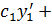 …+
…+ 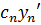 ,
, 
Доказательство (стр. 288, [1]).
Дата добавления: 2015-09-05; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство | | | Замечание |