|
Читайте также: |
Пусть существует производная f 
( 
) т.е. существует предел 
.
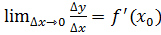Тогда,
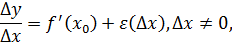
где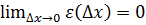 
и, следовательно, для ∆ x ≠ 0, справедливо равенство
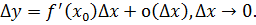
Итак, мы имеем равенство (1.2) при A=f 
( ). Таким образом, функция f дифференцируема в точке .
Подчеркнем, что в теореме 3.1 речь идет о конечной производной.
Таким образом, дифференцируемость функции f(x) в точкеr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">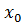 
равносильна существованию в этой точке конечной производной f 
( . ).
Терема 3.2.
Если функция f дифференцируема в некоторой точке, то она и непрерывна в этой точке.
Дата добавления: 2015-09-05; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство необходимости | | | Доказательство |