
Читайте также:
|
Пусть функция f (x) определена в некоторой окрестности точки x0 и пусть x - произвольная точка этой окрестности. Если отношение 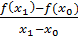 имеет предел при x → x0.,то этот предел называется производной функции f в точке x0 и обозначается f
имеет предел при x → x0.,то этот предел называется производной функции f в точке x0 и обозначается f  (x0 ):
(x0 ):
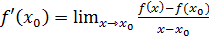 (1.1)
(1.1)
Если ввести обозначение 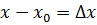 ,то определение (1.1)запишется в виде:
,то определение (1.1)запишется в виде:
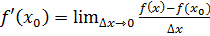 .
.
Полагая 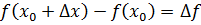 ,получаем ещё одну запись определения производной:
,получаем ещё одну запись определения производной:
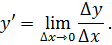
Примеры:
Используя определение, найти производную функции:
1. 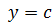 ( (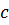 -постоянная).
Так как ∆ -постоянная).
Так как ∆ 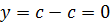 ,то ,то 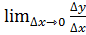 = 0, и, таким образом, = 0, и, таким образом, 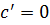 .
2. .
2. 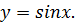
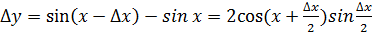 , ,
 = cos x.
(sin x)'= cos x. = cos x.
(sin x)'= cos x.
|
Дата добавления: 2015-09-05; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ф.Энгельс | | | Односторонние производные. |