Аппроксимация сигналов с ограниченным спектром рядом Котельникова. Теорема Котельникова.

Постановка задачи:

Пусть задан сигнал x(t):

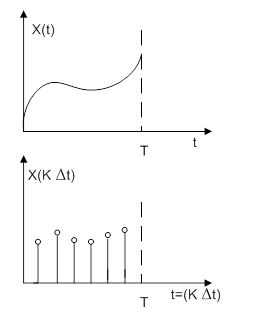
Теорема Котельникова: Любой сигнал x(t) состоящий из частот от о до fв можно представить с любой точностью при помощи чисел следующих друг за другом через 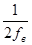секунд.

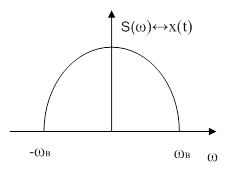
Сигнал с непрерывным ограниченным спектром 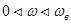полностью определяется дискретными значениями, взятыми через интервал .

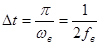Доказательство сводится к разложению сигнала в ряд специального вида (в Ряд Котельникова):

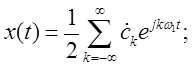
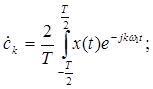
Представим сигнал x(t) интегралом Фурье:

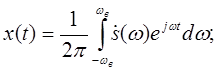(1)

Представим 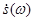рядом Фурье:

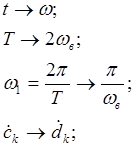
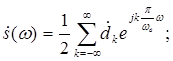(2)

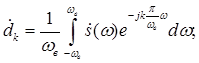(3)

Подставим выражение (2) в выражение (1):

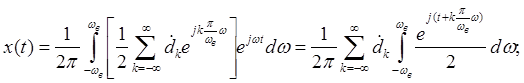
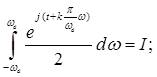
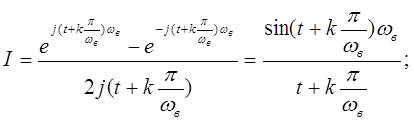
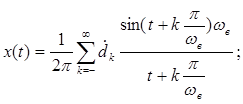(4)

Формулу (1) запишем в виде:

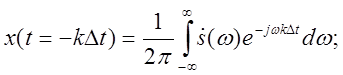(5)

Сравним выражения (5) и (3), принимая во внимание, что .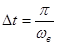

Поделим выражение (3) на (5):

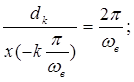
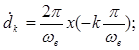
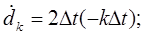
Тогда выражение (4) примет вид:

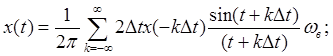
1)

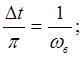
2) Поменяем знак индекса:

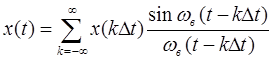- представление сигнала рядом Котельникова.

Обозначим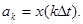

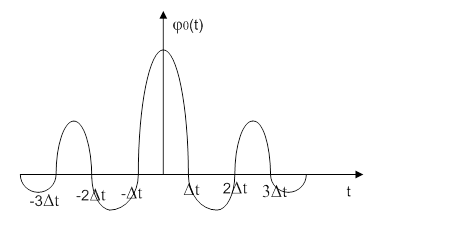
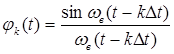- функция отсчетов.

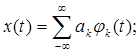
Сигнал x(t) представленный по заданной системе базисных функций 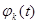полностью определяются совокупностью коэффициентов выступают отсчеты сигнала, следующих через 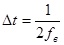секунд, т.е. сигнал полностью определяется этими отсчетами. Этим теорема доказана.

Свойства функции отсчетов:

1. Система ортогональна на интервале .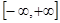

2.

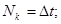
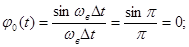
Все реальные сигналы имеют бесконечный спектр.

Замечания по теореме Котельникова:

1. Теорема дает строгое обоснование возможности восстановления сигнала по дискретным отсчетам.

2. Для восстановления сигнала необходим идеальный фильтр.

3. Сигнал должен иметь непрерывный спектр, при дискретном спектре справедливость теоремы нарушается.

Дата добавления: 2015-09-04