Читайте также:
|
Е – случайные события. Ω – эксперимент.
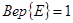- достоверное событие.
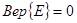- невозможное событие.
- случайная величина – это величина, которая может принять то или иное значение из возможных.
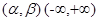- область возможных значений.
Квантиль – значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Единственный корень уравнения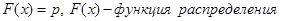 
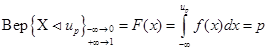- функция распределения вероятностей.
это теоретический квантиль.
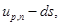выборочный квантиль
Из ГС извлекаем выборку, упорядочиваем элементы в порядке возрастания. далее строим ф-ю распределения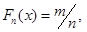 
n-объем выборки, m- число элементов меньше или равных выборочн. фун-ии распред.
Выборочным квантилем уровня р наз-ся единственный корень уравнения
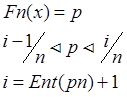
Ent – целая часть от произведения
Св-ва оценок:
они состоятельны
они ассиметричны и нормальны
этот метод не гарантирует несмещенность и эффективность
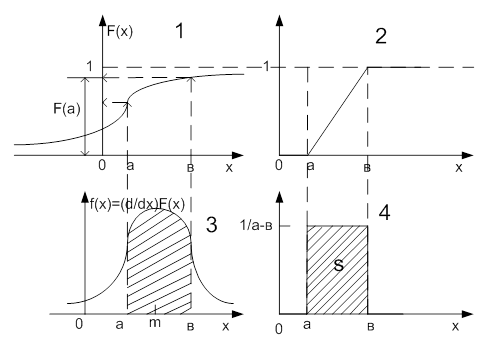
1. Интегральный закон распределения.
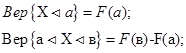
2. 
- плотность распределения вероятности.
3. 
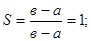
4. Дифференциальный закон распределения.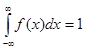 
- условия нормировки.
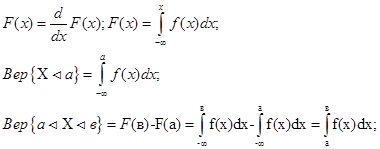
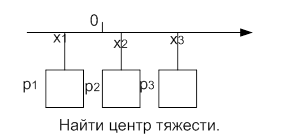
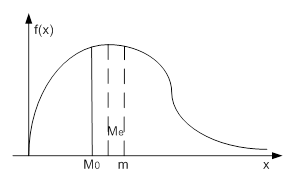
Среди числовых характеристик выделяют характеристики положения и рассеивания. К характеристикам положения относят m, M0, Me (мат. ожидание, мода и медиана).
1. 
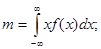- мат. ожидание.
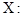
| x1 | x2 | x3 |
| p1 | p2 | p3 |
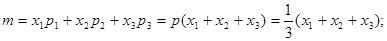
2. 
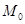- мода.
Это значение, которое встречается максимальное число раз
3. 
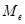-медиана.
Дата добавления: 2015-09-04; просмотров: 104 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ряд Фурье. Три формы. | | | Устойчивость и физическая реализуемость цифровых ЛИВ-систем. |