Случайные последовательности. Общие определения.

Билет 1

Значение обработки экспериментальных данных.

- современные средства позволяют получить большой массив данных, содержащих обширную информацию, которую необходимо обрабатывать;

- выделение скрытых составляющих электрофизиологических процессов, которые обладают значительной информационной ценностью;

- создание качественно новых моделей и алгоритмов, позволяющих повысить полноту отображения и получить принципиально новые признаки биологических объектов

- совершенствование имеющихся алгоритмов с целью увеличения эффективности и снижения требований к аппаратной части;

- создание алгоритмов и моделей, которые позволяют комплексно оценить влияние совокупности факторов на определённые процессы

Случайные последовательности. Общие определения.

Теорией случайных процессов (в дальнейшем СП), называется математическая наука, изучающая закономерности случайных явлений в динамике их развития.

Понятие СП представляет собой обобщение понятия случайной величины (СВ).

СВ – величина, которая в результате опыта со случайным исходом принимает то или иное значение из области возможных. СП x(t) – процесс, значение которого при любом фиксированном t=t0, является случайной величиной x(t0)=x0.

Реализация СП:

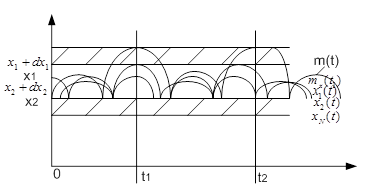
Конкретное проявление СП на данном интервале времени называют реализацией. Зафиксированные в результате эксперимента реализации СП можно описать аналитически. Это будут не случайные, а детерминированные функции времени. Их обозначают

СП можно рассматривать как совокупность, множество или ансамбль его реализаций и обозначать:

Чем больше N, тем глубже и богаче наши знания об изучаемом явлении, тем достовернее будут наши умозаключения.

В частных случаях СП можно задать аналитически в виде случайных функций, т.е. функций, параметры которых СВ: где U – СВ.

Тем не менее, в инженерной практике чаще всего имеют дело с представлением СП, как ансамбле его реализаций.

Поскольку понятие СП представляет собой обобщенное понятия СВ, то для описания СП, можно воспользоваться теми же вероятностными характеристиками, что и для СВ, а именно:

- плотностью распределения,

- функцией распределения,

- моментными функциями.

Введем эти характеристики СП.

Зафиксируем момент времени , получим 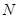значений: .

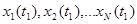Выделим те значения, которые не превосходят уровень Вольт. Посчитаем их число и обозначим . Тогда, вероятность ,очевидно, будет зависеть от и , т.е.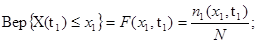

Функция называется одномерной функцией распределения вероятностей СП (одномерный закон распределения).

Производная: - одномерная плотность распределения вероятностей СП.

Одномерна начальная моментная функция k-го порядка: .

Наиболее часто используемая начальная моментная функция 1-ого порядка:

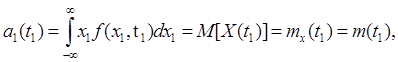которая называется математическим ожиданием СП и представляет собой среднее течение СП.

Одномерная центральная моментная функция k-ого порядка: .

Наиболее часто используемая одномерная центральная моментная функция 2-го порядка, которая называется дисперсией СП:

Автокорреляция СП в 2 различн момента времени t1,t2:

K(t1,t2)=M[x(t1)*x(t2)] определяет вероятностную связь между сечениями

Авто-я центрированного СП, т е с удаленным средним – это автоковариация

C[t1,t2]=M[x(t1)- x_ср(t1)]* M[x(t2)- x_ср(t2)]

Дата добавления: 2015-09-04