Ряд Фурье. Три формы.

Постановка задачи: Пусть x(t) любой периодический сигнал: x(t)=x(t+T);

Первая гармоника сигнала: ω1=2π/Т;

Необходимо разложить сигнал по системе базисных функций:

{φk(t)}={сos k ω1t, sin k ω1t}; (*)

Используя критерий сходимости в среднеквадратическом. Всякий, с несущественными для практики математическими ограничениями (условиями Дирихле), периодический сигнал x(t) с периодом Т=2π/ ω1, может быть представлен рядом по тригонометрическим функциям:

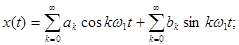
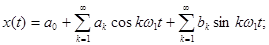(1) – синусно-косинусная форма ряда Фурье

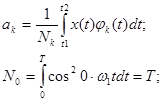
Если коэффициенты ряда (1) найдены по формулам (2), то ряд (1) называется рядом Фурье.

Вещественная форма представления ряда Фурье:

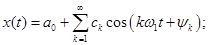(3)

{ak,bk}↔{ck,ψk};

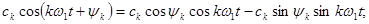
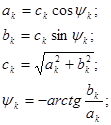
Комплексная форма ряда Фурье:

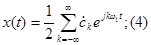, где - комплексная амплитуда.

Зная формула Эйлера:

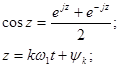
Тогда выражение (3) примет вид:

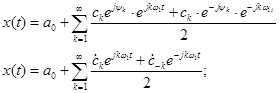
Для общности обозначим:

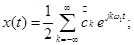
{ck} – спектр амплитуды сигнала x(t);

{ψk}- спектр фаз сигнала x(t);

{ }- комплексный спектр сигнала x(t);

{ }- система базисных функций в виде комплексных экспонент;

{ak,bk}↔{ck…,ψk};

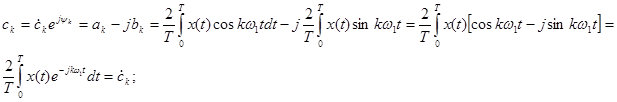
2Цифровые ЛИВ-системы. Импульсная характеристика. Свёртка числовых последовательностей.

Цифровые системы (ЦФ) определяются математически, как однозначное преобразование или оператор, отображающий входную последовательность в выходную.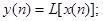

В зависимости от ограничений, накладываемых на оператор L различают несколько классов ЦФ.

Первый класс линейных цифровых фильтров определяется принципом суперпозиций, 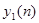является откликом .

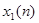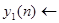
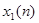
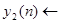
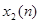
система линейна тогда, когда

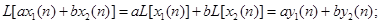
Второй класс инвариантных к сдвигу ЦФ определяется следующим свойством:

;

;

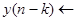
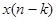нестареющая система – это система с постоянными параметрами

g(n) – отклик системы на единичный импульс

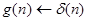- импульсная характеристика фильтра.

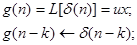
Отклик фильтра на произвольную последовательность обозначенную y(n).

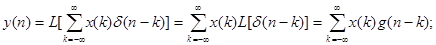
- свертка.

Импульсная характеристика полностью характеризует фильтр.

Легко показать, что:

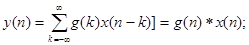
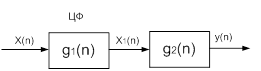
Рассмотрим варианты каскадного включения двух ЦФ.

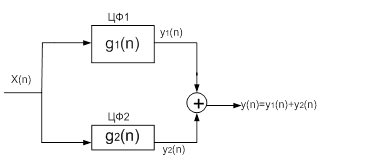
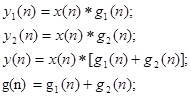
Пример вычисления свёртки

Каждая последовательность , у которой частное отношение двух соседних членов постоянно

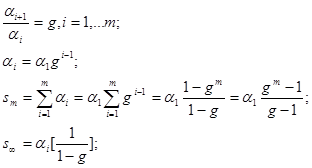
Рассмотрим ЦФ с импульсной характеристикой вида:

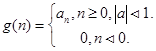здесь очевидно, что а в степени n

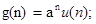
Найдем реакцию на входной сигнал вида:

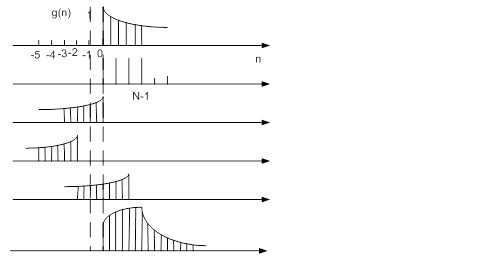
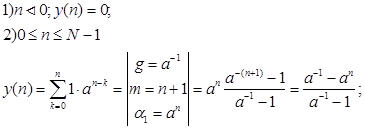
последовательность возрастает

последовательность убывает

Дата добавления: 2015-09-04