Аппроксимация сигналов и критерий приближения

Аппроксимация – это замена одних математических объектов (чисел, функций) другими, более простейшими, в том или ином смысле, близкими к первым. Например, замена кривой ломаной линией – кусочно-линейная аппроксимация.

Введем обозначения:

x(t) – исходная функция;

x*n(t) – аппроксимирующая функция;

Теоретические вопросы, которые приводят к задаче аппроксимации.

1. Пусть функция x(t) – невыражаемая в числах, имеющая некоторые особенности или сложная функция. И мы хотим заменить её аппроксимирующей:

x(t)→ x*n(t)

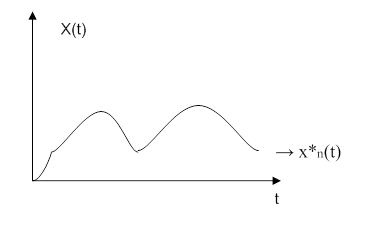
2. На самописце получена реализация, которую нужно аппроксимировать

некоторой функцией:

1. Есть отсчеты сигналов:

ti	x(ti)
t1	x(t1)
t2	x(t2)
…	…

Необходимо перейти к аппроксимирующей функции x*n(t).

Аппроксимирующая функция обычно находится в виде взвешенной конечной суммы линейно независимых функций:

x*n(t)=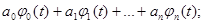

Т.е. x*n(t)=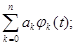

{ak}=const;

{φk(t)} – базисные функции.

Пример базисных функций:

{φk(t)}={1, t, t²,…,tⁿ};

Базисные функции линейно независимы, если ни одна из них не может быть представлена в виде линейной комбинации других функций из этого базиса.

Для решения задачи аппроксимации нужно так подобрать коэффициенты ak, чтобы минимизировать некоторый количественный критерий близости аппроксимирующей функции и исходной

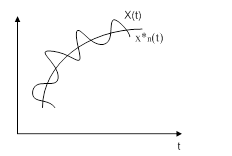
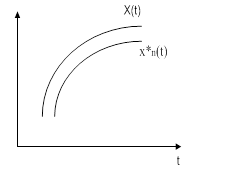
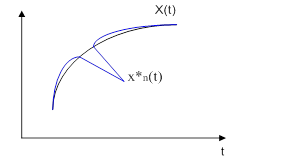
Критерии аппроксимации:

1. Минимизация площади, ограниченной исходной и корреляц-ой функции.
2. Максимальное отклонение должно быть минимальным.
3. Близость производных.

Критерии приближения:

1. Сходимость в каждой точке.

Аппроксимирующая функция сходится к исходной в каждой точке на отрезке [t1,t2], если разность 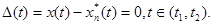Такое возможно только при n=∞.

1. Сходимость в среднеквадратическом.

Аппроксимирующая функция приближается к исходной в среднеквадратическом, если:

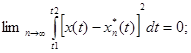
На практике, если этот предел меньше некоторого ε², то он удовлетворяет критерию сходимости в среднеквадратическом.

1. Критерий равномерной сходимости.

Аппроксимирующая функция приближается к исходной равномерно, если:

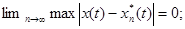
Задачу аппроксимации можно рассматривать как задачу разложения исходной функции по заданному базису.

Для дискретных сигналов критерий сходимости в среднеквадратическом может быть записан следующим образом:

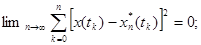
Дата добавления: 2015-09-04