
Читайте также:
|
Постановка задачи:
Задан сигнал x(t) на отрезке времени t=[t1,t2], который необходимо аппроксимировать x*n(t)=∑аkφk(t). Задана система базисных функций: {φk(t)}. Критерий сходимости: среднеквадратический.
Эта задача решается наиболее просто, если система базисных функций {φk(t)} ортогональна.
Система базисных функций {φk(t)}, называется ортогональной на отрезке [t1,t2], если:
1) 
2) 
Nk – называется нормой базисной функции. (здесь надо поставить квадрат во всех Nk, иначе это квадрат нормы)
Если для всех k Nk =1, то такая система базисных функций называется ортогональной и нормированной (ортонормированная).
Запишем критерий сходимости в среднеквадратическом:
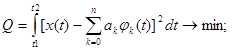
Необходимо найти такие аk, чтобы Q→min для данного n.
Найдем частную производную от Q по aj:


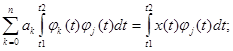


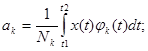
В некоторых случаях удобно использовать базисные системы функций ортогональных с весом {ψk(t)}.
Система называется ортогональной с весом, если:
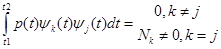
От функции ортогональной с весом легко перейти к функциям ортогональным без веса: {ψk(t)}→ {φk(t)}.
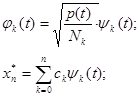
Необходимо найти ск:
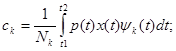
Дата добавления: 2015-09-04; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оценивание параметров распределения генеральной совокупности методом максимального правдоподобия. | | | Типовые числовые последовательности |