Читайте также:
|
Наиболее мощный метод, наиболее полно учитывает информацию несомую выборкой.
Имеем ГС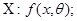 
;
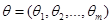Извлекается выборка: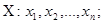 
Составляется функция правдоподобия: 
Функция правдоподобия характеризует вероятность появления именно той выборки, которая получена в эксперименте. Если необходимо по выборке оценить вектор θ, то естественно взять в качестве оценок 
, такие, которые бы имели максимальную вероятность.
Из соображений удобства вычисляют функцию правдоподобия.
Рассмотрим ее логарифм:
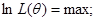
Для нахождения оценок, находятся частотные производные.
Пусть имеем нормальную ГС:
ГС 
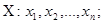
Перейдем к логарифмической функции:
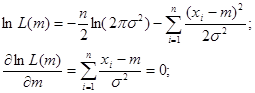
- оценка максимального правдоподобия мат. ожидания нормально распределенной ГС.
- выборочная средняя.
Проверка на несмещенность:
1) 
- доказать.
- оценка несмещенная.
2)Состоятельность оценки.
3)Требования эффективности.
Получена эффективная оценка.
Пример:
P – вероятность появления событий Е в случайном эксперименте Ω. Пусть проведено n отсчетов, событие Е произошло в ν случаях.
Доказать, что частота событий 
- есть оценка максимального правдоподобия.
Введем вспомогательную величину 
| X | ||
| вер | p | (1-р) |
Дата добавления: 2015-09-04; просмотров: 60 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аппроксимация сигналов и критерий приближения | | | Аппроксимация сигналов системами ортогональных функций |