Читайте также:
|
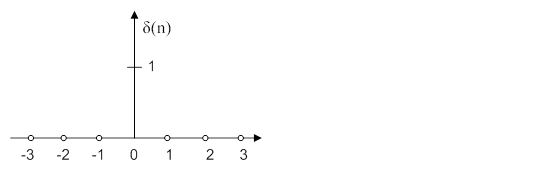
1. Единичный импульс:
2. Единичный скачек:
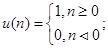
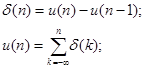
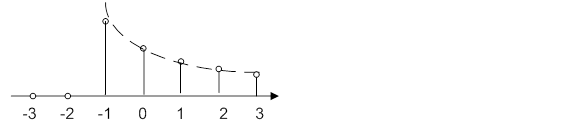
3.Действительная экспоненциальная последовательность:
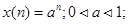
Гармоническая последовательность:
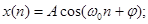
4.Комплексная экспоненциальная последовательность:
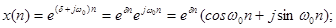
Последовательность x(n) называется периодической с периодом N, если x(n)=x(n+N) для всех n.
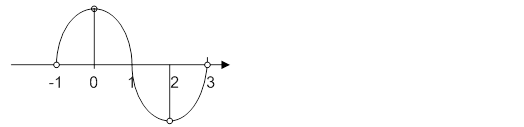
Рассмотрим пример:
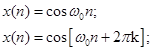Косинус – периодическая функция.
При k=1,ω0N=2π.
Тогда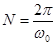 
- целое число.
Пусть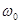 
такое, что 
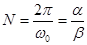- рациональное число.
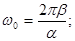
Пример: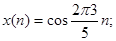 
Пусть 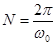- иррациональное число. У такой последовательности периода нет.
Параметр 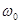будем называть частотой гармонической последовательности или комплексной экспоненты независимо от того являются ли эти последовательности периодическими.
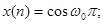
Будем рассматривать -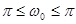 
, все остальные значения не приносят новой информации, т.к. n целое число.
Рассмотрим непрерывный гармонический сигнал:
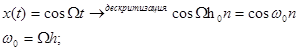
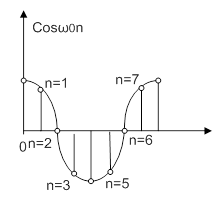
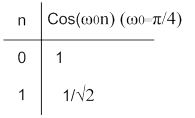
Пусть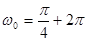 
Энергия числовой последовательности:
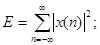
Произвольная последовательность:
Дата добавления: 2015-09-04; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аппроксимация сигналов системами ортогональных функций | | | Ряд Фурье. Три формы. |