Анализ вариационных рядов распределения

Анализ вариационных рядов распределения следует провести на основе следующих показателей:

1. Средний уровень ряда распределения:

2. Среднее квадратическое отклонение:

i =1,32;

3. Моменты:

первого порядка:

m ₁=

второго порядка:

m ₂= ;

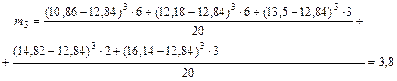
4. Коэффициенты:

ассиметрии:

;

k_a =

эксцесса:

;

k_э =

5. Структурные средние:

моды:

Mo =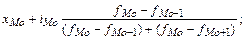

Mo =

медианы:

Me = ;

Me =

Построить расчетную таблицу по следующей схеме:

Таблица 1. – Расчет показателей для определения центральных моментов.

Интервал	Частота, f	X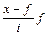
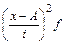
10,2–11,52 11,52–12,84 12,84–14,16 14,16–15,48 15,48–16,8		10,86 12,18 13,5 14,82 16,14	–9 –3 1,5 7,5	13,5 1,5 0,75 4,5 18,75	–20,25 –0,75 0,375 6,75 46,875	25,3125 0,375 0,1875 10,125 117,1875
Итого:		–				153,187

Примечание:

Вероятность того, что исследуемое распределение соответствует закону нормального распределения, устанавливается, исходя из следующих критериев:

1. При симметричном нормальном распределении .

Если k_a >0, , то в распределении имеется правостороннее распределение (положительный эффект).

Дата добавления: 2015-09-05