Анализ интенсивности экономического развития, его тенденции, закономерности

Исследование интенсивности динамических процессов производится путем анализа уровней ряда динамики. Для этого вычисляются такие показатели, как абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста, средний уровень ряда, средний абсолютный прирост и средний темп роста и прироста.

Показатели анализа ряда динамики следует представить в табличной форме:

Таблица 9 – Анализ показателей динамики

Показатели	Временной интервал	В среднем
Уровень динамического ряда, ед.	10,6	14,3	12,1	15,6	17,9	14,1
Абсолютный прирост:
Базисный	–	3,7	1,5	5,0	7,9	1,82
Цепной	–	3,7	–2,2	3,5	2,3	1,82
Темп роста:
Базисный	100,0	134,9	114,1	147,2	168,9	114,0
Цепной	–	134,9	84,6	128,9	114,7	114,0
Темп прироста:
Базисный	–	34,9	14,1	47,2	68,9	14,0
Цепной	–	34,9	–15,4	28,9	14,7	14,0
Значение 1% прироста (цепной способ)	–	0,106	0,143	0,121	0,156	0,13

Для определения основной тенденции развития ряда динамики применяется метод аналитического выравнивания. Суть его состоит в том, что основную тенденцию развития можно представить в виде математической функции:

уравнение прямой, параболы второго порядка, степенной функции, гиперболы и др. Параметры уравнения определяются методом наименьших квадратов.

Для уравнения прямой система нормальных уравнений имеет вид:

Параметры уравнения определяются путем решения системы нормальных уравнений или по формулам:

a ₁= ;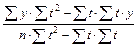

a ₀

Для определения параметров уравнения прямой строится расчетная таблица:

Таблица 10 – Расчет показателей для определения уравнения прямой линии

Год	Эмпирические уравнения	T	yt	t^2
…….
Сумма

Если нумерация лет производится так, чтобы =0, то параметры уравнения определяются по формулам:

;

.

Кроме того, для изучения тенденции развития возможно исследование цепных абсолютных приростов и коэффициентов роста. При этом расчетные формулы имеют следующий вид:

;

;

Иногда для уравнения тренда подходит одновременно несколько функций. Отбор наилучшей функции производится по величине остаточной дисперсии (отклонения теоретических уровней от эмпирических), которая вычисляется по формуле:

;

Построенные трендовые модели можно использовать для прогнозирования. Осуществляя прогноз, важно давать не только точечную оценку, но и интервальную с учетом погрешности прогноза.

Погрешность может быть представлена в виде доверительного интервала.

;

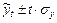где – среднее квадратическое отклонение ошибки тренда;

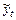– теоретические значения уровней ряда;

t – значение статистики Стьюдента (р =0,05; р =0,01).

Если t – период упреждения (прогноза) будет равен t = i + 1, то доверительный интервал прогноза будет иметь вид:

,

где – среднее квадратическое отклонение прогноза.

Среднее квадратическое отклонение прогноза вычисляется по формуле:

где – среднее квадратическое отклонение теоретических данных от имперических;

n – число наблюдений;

t ₁ – период времени, для которого производится прогноз (период упреждения),

t ₁ = n + 1;

– значение порядкового номера уровня, стоящего в середине ряда динамики.

Так как время нумеруется (t = 1, 2,... n), то

.

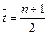Дата добавления: 2015-09-05