
|
Читайте также: |
Методика проведения многофакторного корреляционного анализа основывается на тех же принципах, которые характерны для однофакторного корреляционного анализа. Вместе с тем необходимо тщательно отобрать для анализа наиболее важные и существенные показатели, предварительно исчислив по каждому признаку показатели вариации.
С целью установления существенности влияния факторных признаков на результативный следует исчислить и проанализировать коэффициент регрессии, парные коэффициенты корреляции и критерии их достоверности. Далее необходимо составить уравнение множественной регрессии, предварительно установив тип функции.
Уравнение множественной линейной регрессии с тремя переменными имеет следующий вид:
y = a 0 + a 1 x 1 + a 2 x 2
y = –20,8 + 1,69 x 1 – 0,872
Для определения параметров уравнения может быть применена следующая система нормальных уравнений:


Для решения системы нормальных уравнений по исходным данным необходимо вычислить  ,
,  ,
,  ,
, 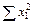 ,
,  .
.
Результаты расчетов занести в таблицу 8.
Таблица 8 – Расчет показателей для определения параметров уравнения множественной регрессии
| Предприятия | Заработная плата | Норма выработки | ПТ | Расчет показателей для определения параметров уравнения множественной регрессии | |||
| y | x 1 | x 2 | yx 2 | x 1 x 2 | 
| 
| |
Продолжение табл. 8
| Итого |
Решение системы нормальных уравнений:
Уравнение множественной регрессии имеет следующий вид:
 – 20,8 + 1,69 x 1 – 0,8 x 2
– 20,8 + 1,69 x 1 – 0,8 x 2
Коэффициент множественной корреляции для двухфакторной линейной модели исчислить по формуле:
 ;
;
ryx 1 = 0,98; ryx 2 = – 0,038; rx 1 x 2 = – 0,28; Ryx 1 x 2 = 0,9037.
Статистическую оценку параметров уравнения множественной регрессии на их значимость оценить t – критерием Стьюдента:
 ;
;
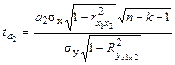 ,
,
где k – число факторов уравнения регрессии.
 8,6949
8,6949
 – 0,3355
– 0,3355
Достоверность коэффициента множественной корреляции определить по формуле:

tR = 19,722
Фактическое значение (tфакт) критерия сопоставить с табличным (tтабл) при заданном уровне вероятности и числе степеней свободы и сделать краткие выводы.
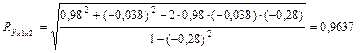



При числе степеней свободы: f = k – (p +1)
f = 20 – (3 +1) = 18
при значимости 0,18 tтабл = 2,8784
Дата добавления: 2015-09-05; просмотров: 143 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Однофакторный корреляционный анализ | | | Анализ интенсивности экономического развития, его тенденции, закономерности |