Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Линейные разностные уравнения с постоянными коэффициентами.

Структура автоматизированных систем сбора и обработки информации | Корреляционные функции СП. Свойства. | Свойства корреляционной функции. | Аппроксимация сигналов и критерий приближения | Оценивание параметров распределения генеральной совокупности методом максимального правдоподобия. | Аппроксимация сигналов системами ортогональных функций | Типовые числовые последовательности | Ряд Фурье. Три формы. | Оценивание распределения параметров генеральной совокупности методом квантилей | Устойчивость и физическая реализуемость цифровых ЛИВ-систем. |


Читайте также:
  1. I.4. Состояния системы. Уравнения состояния системы.
  2. Аналитическое решение дифференциального уравнения
  3. Всякая лин. Комбинация решений ЛОДУ является решением этого уравнения или системы.
  4. Вывод дифференциального уравнения
  5. Вывод уравнения
  6. Графический способ решения IRR — уравнения
  7. Двигатели с постоянными магнитами

Важным подклассом ЛИВ – систем являются фильтры, для которых вход x(n) и y(n) удовлетворяют линейному разностному уравнению n-го порядка с постоянными коэффициентами вида:

 

Вводя новые ограничения, запишем:

ИХ фильтра с таким уравнением бесконечна

 

Изобразим структурную схему фильтра, описанную этими уравнениями:

 

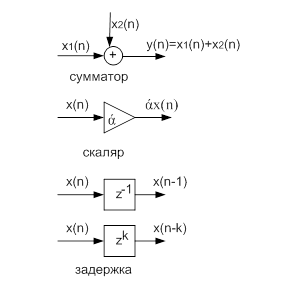
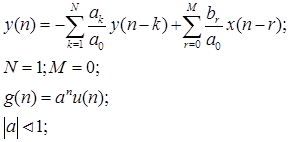
В общем случае ЦФ может иметь импульсную характеристику, как конечной, так и бесконечной характеристики. Такие фильтры называются БИХ и КИХ-фильтры.

Тогда:

Пример: М=1.

Структурная схема фильтра:

Найдем импульсную характеристику:

 

 

 

Дата добавления: 2015-09-04; просмотров: 77 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Спектр типовых импульсных сигналов| Билет 8.
mybiblioteka.su - 2015-2024 год. (0.007 сек.)