Читайте также:
|
Синусоидальная последовательность и последовательность типа комплексная экспонента являются собственными функциями ЛИВ систем, поэтому отклик будет иметь ту же форму.
Рассмотрим специальный класс входных последовательностей (комплексная экспонента). Покажем, что она является собственной функцией ЛИВ системы дискретного времени, т.е. проходя через ЛИВ систему комплексная экспонента не меняет свою форму, а меняет модуль и фазу.
Таким образом, для выбранного класса входных последовательностей выход совпадает со входом с точностью до комплексного множителя, который выражается через импульсную характеристику
- частотная характеристика ЦФ.
, отсюда ясно, что 
описывает изменение комплексной амплитуды комплексной экспоненты, как функции частоты ω.
Свойства частотной характеристики:
1)Частотная характеристика – это непрерывная функция частоты ω, причем периодическая с периодом 2П. Обычно ее рассматривают на отрезке 
2)Частотная характеристика может быть представлена: 
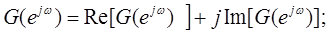
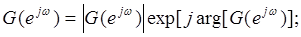
Если импульсная характеристика действительна, то модуль частотной характеристики четная функция, а аргумент нечетная функция частоты ω и наоборот.
Т.к. функция периодическая, то 
Пример: Пусть дан ЦФ со следующей характеристикой:
По определению:
Импульсная характеристика представляет собой коэффициенты Фурье периодической функции 
, т.е. 
.
Рассмотрим произвольную числовую последовательность 
:
- прямое преобразование Фурье числовой последовательности x(n).
Тогда: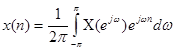 
- обратное преобразование Фурье числовой последовательности x(n).
Дата добавления: 2015-09-04; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аппроксимация сигналов с ограниченным спектром рядом Котельникова. Теорема Котельникова. | | | Эффект наложения спектров. Частота Найквиста |