Предел функции при х ->а и при х->∞.Геометрическая интерпритация предела функции.Односторонние пределы.

Прямая в пространстве.Общие,параметрические и канонические уравнения прямой в пространстве.Взаимное расположение прямых в пространстве.Точка пересечения прямой и плоскости в пространстве.Взаимное расположение прямой и плоскости в пространстве.

-Прямая, являющаяся линией пересечения 2 плоскостей, задается системой уравнений:

Положение прямой в пространстве определено,если задана точка М₀ на прямой и вектор S параллельный этой прямой(лежащий на этой прямой)S-направляющий вектор прямой.ПустьS={m,n,p)Векторное ур-е прямой :r=r₀+t*S,где S,r,r₀-векторы.

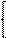-Параметрическое ур-е прямой: r={x,y,z}, r₀={x₀,y₀,z₀}, t*S={t_m,t_n,t_p}, то ур-е: х=х₀+mt

Y =y₀+nt y=y₀+tn

Z=z₀+pt
-каноническое уравнение прямой в пространстве
-Ур-е прямой проходящей через 2 точки:х-х₁\х₂-х₁=y-y₁\y₂-y₁=z-z₁\z₂-z₁

-Условие парал-ти 2 прямых: S₂ ||S,то m₁\m₂=n₁\n₂=p₁\p₂

-Условие перпендикулярности 2 прямых: S₁_|_S₂,еслиS₁*S₂=0
Прямая и плоскость в пространстве могут:
а) не иметь общих точек;
б) иметь ровно одну общую точку;
в) иметь хотя бы две общие точки.
Точка пересечения прямой и плоскости
13)Переменная.Функция,область ее определения.Способы задания функции.Важнейшие свойства функции:четность,нечетность,периодичность,наличие обратной функции.Классификация.

Если к каждому значению х из множества Х поставлено в соответствии по определенному правилу f единственное значение переменной y из множества Y,то говорят,что задана функция y=f(x), определенная на множ-ве Х с областью значения Y.

х-аргумент,y-функция.Х-ООФ,Y-ОЗФ.

Способы задания функции:1)Табличный(используется если множество Х конечно) 2)Графический (Графиком функции y=f(x) называется множество точек с координатами (x,y), где х принадлежит Х,yпринад. Y) 3)Аналитический: а)в явном виде(y=f(x)) б) в неявном виде (F(x,y)=0)пример: х²+y²=4 в)параметрическизаданнаx=x(t) y=y(t)
Функция y=f(x), область определения которой симметрична относительно начала координат называется четной, если y(-x)=y(x) Нечетной,еслиy(-x)=-y(x).

Функция y=f(x) называется периодической,еслисуществуетчислоТ,такое что f(x+T)=f(x)

Пусть дана ф-я y=f(x),где х ϵ Х, yϵY,если любому значению yϵY ставиться соответ. значение х ϵ Х,такое что y=f^-1(x),то говорят что задана функция х=y(f),которую называют обратной.

Отображение y=f(x) называется взаимооднозначным,если разным значениям х соответствуют разные значения y.

Классификация ф-ий: 1)Элементарные а)степенные б)показательные в)тригонометрические (y=sinx) г)обратные тригонометрическим д)логарифмические.Элементарныеделяться на:1)алгебраические а)многочлен. б)рациональная дробь в)ирроциональная г)модуль перемен. 2)Трансцедентные а)логарифмич. б)показат. в)тригонометр. – гипорболическийсинус,косинус, тангенс и катангенс.

Предел функции при х ->а и при х->∞.Геометрическая интерпритация предела функции.Односторонние пределы.

Пусть ф-я y=f(x) определена на некотором множестве Х,а-фиксированная точка на оси ОХ.Точка а может принадлежать, не принадлежать оси ОХ.Дельта окрестностью точки а называют интервал |х-а|<δ,где δ-окрестность(U_a). Пусть ф-я y=f(x) определена на некотором множестве Х,а-фиксированная точка на оси ОХ,число В называется пределом ф-и y=f(x) в точке а или при х->а. Если для любого числа ε>0 существует такое число,зависящее от δ,что для всех х удовлетвор.неравенству 0<|х-а|<δ выполняется неравенство f(x)=B<ε.Определение означает,что если lim f(x)=B,то всегда найдется дельта-окрестность такая,что значения ф-и для х из этой окретности сколь угодно мало отличное от В.

Число В называется пределом ф-и y=f(x) при х->∞,если для любого ε>0 существует такое число δ зависящее от ε>0,что при всех х удовлетворяющих неравенству |х|>δ,выполняется неравенство |f(x)-B|<ε.

Предел слева от точки х=а, справа.

Дата добавления: 2015-09-04