Читайте также:
|
Предположим,что функция f(x), непрерывна в промежутке
[ 
] (H>0) и имеет конечную производную f’(x) для x> 
.Если существует (конечный предел или нет) предел
,то такова же будет и производная в точке справа. Действительно, при 0 < ∆ x ≤ H имеем равенство 
.Так как аргумент c производной содержится между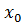 
и 
,то при ∆ x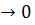 
он стремится к 
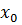,так что правая часть равенства, а с нею и левая стремится к пределу K,что и требовалось доказать. Аналогичное утверждение устанавливается и для левосторонней окрестности точки .
Рассмотрим в качестве примера функцию
f 
(x)=x 
arcsin x + 
В промежутке [-1,1].если -1<x<1,то обычным правилам дифференциального исчисления легко найти:
f (x)=arcsin x.
При x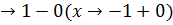 
эта производная, очевидно, стремится к пределу 
; значит и при x= ± 1 существуют (односторонние) производные:
f (± 1)= ± 
.
Если вернуться к функциям 
, 
,которые мы рассматривали, то для них (при 
) имеем:
, 
Так как первое из этих выражений при 
стремится к +∞, а второе при 
имеет, соответственно, пределы ± ∞,то заключаем сразу, что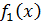 
в точке x=0 имеет двустороннюю производную +∞. В то время, как для 
в этой точке существуют лишь односторонние производные: справа +∞ и слева -∞. Из сказанного вытекает также, что, если конечная производная f (x) существует в некотором промежутке, то она представляет собой функцию, которая не может иметь обыкновенных разрывов или скачков: в каждой точке она либо непрерывна, либо имеет разрыв второго рода.
Дата добавления: 2015-09-05; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Замечание . | | | Теорема Коши.6.5 |