Читайте также:
|
1.Определить промежутки, на которых функция:
возрастает и убывает в строгом смысле.
Находим производную функции 
.
Из неравенств 
и получаем,что данная функция возрастает на 
и убывает на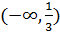 
.
2.Определить промежутки возрастания и убывания функции: 
.
Находим производную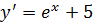 
.
Поскольку 
при всех x, то и 
на всей числовой оси. Следовательно, данная функция строго возрастает на всей оси (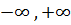
).
Дата добавления: 2015-09-05; просмотров: 46 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Замечание. | | | Определение 8.1. |