Замечание. Подстановка приводит интеграл

Подстановка приводит интеграл

к одному из следующих ,

Замечание. Если в выражении, содержащем указанные радикалы, присутствует в нечетной степени, то вполне эффективной может оказаться замена или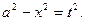

Пример 52.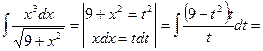

Биномиальные дифференциалы т.е. дифференциалы

вида где и 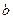- постоянные, отличные от 0, а - рациональные числа.

Первообразная функции является элементарной функцией в следующих трех случаях:

1) -целое число (замена где -общий знаменатель дробей и

2) -целое число (замена где -знаменатель

дроби

3) -целое число (замена где

- знаменатель дроби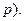

Пример 53.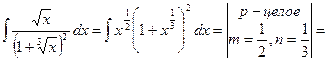

Метод нахождения последнего интеграла подробно описан в разделе “ ДРОБНО-РАЦИОНАЛЬНЫЕ ФУНКЦИИ“.

Дата добавления: 2015-09-01