Замена переменной ( метод подстановки )

Замена переменной или метод подстановки является одним из основных методов интегрирования. Нередко приходится прибегать к подстановке в процессе вычисления интегралов другими методами.

Пусть функция непрерывна, функции , взаимно обратны и непрерывно дифференцируемы, тогда

Функция подбирается таким образом, чтобы подинтегральное выражение приняло более удобный для интегрирования вид.

При применении подстановки главная трудность состоит в том, чтобы получить подинтегральную функцию 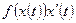, первообразная которой известна.

Излишне упоминать о том, что не каждая подстановка ведет к упрощению. Когда подстановка выгодна и какую именно подстановку следует применить и рассматривается далее.

3.1.Интеграл вида При вычислении интегралов этого вида целесообразна замена

Интеграл вида 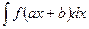заменой приводится к интегралу

Пример 11.

=

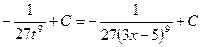
Пример 12.

3.2.Интегралы вида ,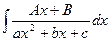

заменой 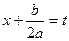приводят к интегралам

Вычисление этих интегралов в зависимости от знака числа сводится к вычислению интегралов вида

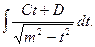
Каждый из них представляет собой сумму двух интегралов, один из которых табличный, а другой вычисляется подведением под знак дифференциала (см. примеры 4,5).

Замечание. В частном случае

(См. также пример 9).

Пример 13.

3.3. Интегралы вида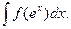

Пример 14.

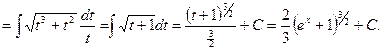
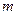3.4. Интегралы вида где и 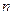-целые числа, замено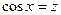й или приводится к интегралу от рациональной функции относительно переменной

Пример 15.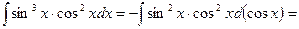

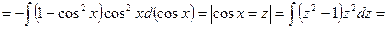
Рассмотрим еще несколько примеров.

Пример 16.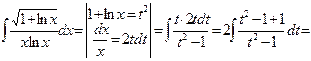

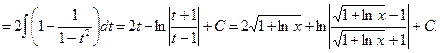Пример17.

Пример 18.

=

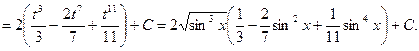
Пример 19.

Пример 20.

Более сложные замены будут рассмотрены далее.

Дата добавления: 2015-09-01