Читайте также:
|
(метод введения нового аргумента)
Таблица интегралов справедлива независимо от того, является ли переменная интегрирования независимой переменной или функцией (инвариантность формул интегрирования).
Если 
где функция 
непрерывна вместе со своей производной 
.
Преобразование подинтегрального выражения к такому виду называется подведением под знак дифференциала.
Таким способом можно найти многие интегралы, не прибегая к более сложным методам.
Так как 
, то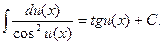 
Пример 3. 
Пример 4. 
Пример 5.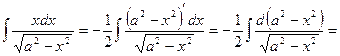 
Пример 6. 
Пример 7. 
Пример 8. 
= 
Пример 9. 
Пример 10. 
Дата добавления: 2015-09-01; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Непосредственное интегрирование | | | Замена переменной ( метод подстановки ) |