Тригонометрические функции

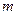2.1. Интегралы вида где и 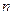-целые числа, вычисляются с помощью искусственных преобразований или применением формул понижения степени. Если хотя бы одно из чисел 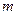или 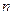нечетное, то данный интеграл замено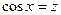й или приводится к интегралу от рациональной функции (см. 3.4). Есл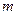и и 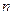четные числа, то возможно применение следующих формул:

Пример 34.

Пример 35.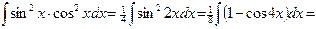

2.2. Интегралы вида находятся с помощью следующих формул:

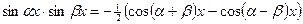
Пример 36.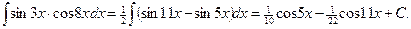

2.3. Интегралы вида где 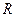- рациональная функция, в общем случае приводятся к интегралам от рациональных функций с помощью универсальной подстановки

Замечание. Если выполнено равенство или ,

то целесообразно применить подстановку или

Замечание. Если выполнено равенство

,то целесообразно применить подстановку

.

Пример 37.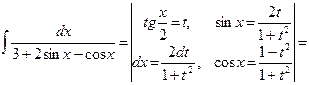

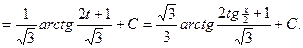
Пример 38.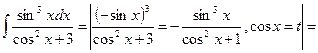

Пример 39.

Замечание. Иногда удобно разделить числитель и знаменатель на .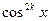

Пример 40 (см. пример 39):

Замечание. Не следует догматически применять приведенные выше правила. Рекомендуемая замена приводит интеграл к довольно сложному интегралу , тогда как универсальная подстановка позволяет вычислить его легко и просто:

Этот же интеграл можно найти и другим способом:

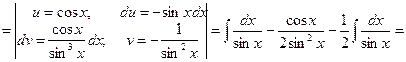
Дата добавления: 2015-09-01