Утверждение 1.4

Если

то правильную дробно-рациональную функцию 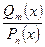можно представить в виде суммы простейших рациональных дробей:

причем сумма содержит столько слагаемых,сколько множителей, с учетом их кратности, в разложении многочлена

Для нахождения коэффициентов разложения

могут быть использованы следующие способы.

Способ соответствующих коэффициентов. Умножаем тождество (*) на 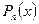и получаем равенство многочленов 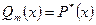. После этого, приравнивая коэффициенты при соответствующих степенях , получаем систему алгебраических уравнений для определения коэффициентов разложения.

Способ частных значений. Умножаем тождество (*) на 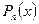и приходим к равенству 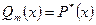. Придавая подходящие конкретные значения, получаем систему уравнений для нахождения коэффициентов разложения.

Замечание. Иногда для определения коэффициентов разложения вышеуказанные способы комбинируют..

После разложения правильной дробно-рациональной функции 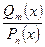её интегрирование сводится к интегрированию простейших рациональных дробей:

подстановкой

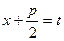
сводится к линейной комбинации интегралов

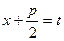подстановкой сводится к линейной комбинации интегралов

и .

Первый из этих интегралов (см. пример 6).

Второй интеграл можно вычислить с помощью следующей рекуррентной формулы:

.

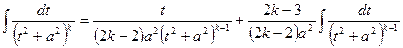Пример 29. .

Подинтегральная функция является правильной рациональной дробью, поэтому она представима в виде суммы простейших рациональных дробей:

. Умножим обе части последнего равенства на 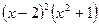и получим равенство

.

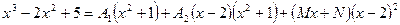Принимая и сравнивая коэффициенты при и свободном члене, имеем:

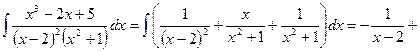
Пример 30. .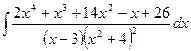

Подинтегральная функция – правильная рациональная дробь – представима в виде суммы простейших рациональных дробей:

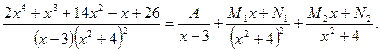
Умножая обе части на 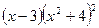, имеем:

=

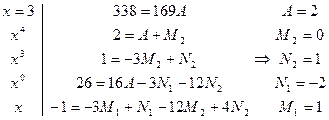
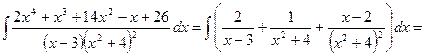
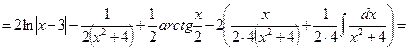
Пример 31.

Разложение на простейшие дроби часто требует громоздких выкладок, поэтому не следует пренебрегать возможностью упростить вычисления с помощью алгебраических преобразований, замены переменной и других известных методов.

Пример 32.

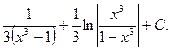
Дата добавления: 2015-09-01