|
Читайте также: |
Дробь 
где 
и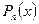 
- многочлены, называется дробно-рациональной функцией (рациональной дробью).
Дробь правильная, если 
и неправильная при 
В случае интегрирования неправильной дроби необходимовыделить целую часть этой дроби. При этом вычисление интеграла сводится к интегрированию многочлена и правильнойдроби.
Рациональные дроби вида
, 
называются простейшими рациональными дробями.
Интегрирование правильной рациональной дроби сводится к интегрированию суммы простейших рациональных дробей.
Имеют место следующие утверждения.
Дата добавления: 2015-09-01; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование по частям | | | Утверждение 1.4 |