|
Читайте также: |
Если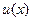 
и 
непрерывно дифференцируемые функции, то справедлива формула 
Суть применения этого метода состоит в том, что при удачном выборе 
и 
вычисление интеграла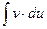 
оказывается проще, чем 
Метод применяется, если под знаком интеграла стоит произведение “ разнородных “ функций, например, 
и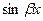 
, и 
, и 
, а также, если подинтегральное выражение содержит логарифмическую или обратные тригонометрические функции и некоторые другие функции.
Пример 21. 
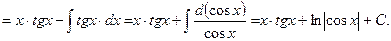
Пример 22. 
Пример 23. 
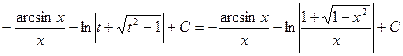
(см. пример 19).
Пример 24. 
Пример 25. (Возвратный интеграл).
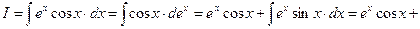
откуда 
Примечание. Интегралы типа 
и 
удобно вычислять с помощью неопределенных коэффициентов. Пример 26. 
Дифференцируем это равенство и приравниваем коэффициенты при функциях 
и 
.
Следовательно,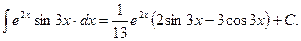 
Пример 27. 
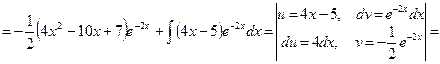
Примечание. При решении примеров такого типа можно также применить метод неопределенных коэффициентов.
Пример 28. 
.
Дата добавления: 2015-09-01; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Замена переменной ( метод подстановки ) | | | Дробно-рациональные функции |