Неопределенные интегралы

Типовой расчет

ВВЕДЕНИЕ

Функция 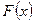,определенная и непрерывная на том же множестве, что и функция 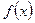, называется первообразнойфункции , если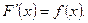

Очевидно, что если 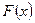-первообразная функции , то 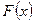+С, где С-произвольная константа, также является первообразной .

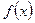Имеет место следующее утверждение: две первообразные одной и той же функции отличаются друг от друга только на некоторую постоянную.

Следовательно, если 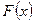- первообразная функции 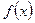, то множество всех первообразных функции 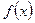имеет вид 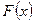+С.

Множество всех первообразных функции 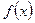называется неопределенным интегралом от функции 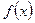и обозначается

Обычно пишут где 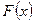-любая перво-образная функции 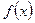. Интеграл может быть записан в любом из видов:

Отсюда видно, что операция нахождения интеграла от данной функции, называемая интегрированием, является действием, обратным дифференцированию.

Дата добавления: 2015-09-01