Дифференциальное уравнение изогнутой оси прямого бруса и его интегрирование

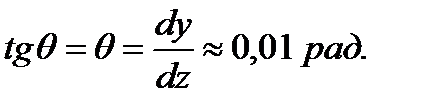При выводе формулы для определения нормальных напряжений при изгибе была получена зависимость: Анализ формулы показывает, что при чистом изгибе записанное выше выражение будет величиной постоянной. Это значит, что ось бруса будет изгибаться по радиусу окружности. Решение уравнения (его интегрирование), вызывает определенные трудности.
Поэтому в инженерной практике используют так называемое приближенное дифференциальное уравнение. Его получают за счет следующих упрощений. • Прогибы на практике малы.Следовательно, и углы поворота малы:

Поэтомуквадратом первой производной пренебрегаем

Проинтегрируем приближенное дифференциальное уравнение и получим: для угла поворота

для прогиба

Для вычисления интегралов, входящих в полученные выше выражения, необходимо:

• начало координат разместить в левой крайней точке бруса;

• брус разбить на участки и записать для каждого участка аналитические выражения для изгибающего момента;

Дата добавления: 2015-09-04