
|
Читайте также: |
Производной y=f(x) в точке х называется предел отношения приращения функции Δy к прирощению аргумента Δх, когда Δх->0,если этот предел существует и конечен.
LimΔy\Δх при Δх->0=y`.
Геометрический смысл производной:y=f(x) – это tg угла наклона касательной к графику y=f(x) т.е. y`=tgα=k
Механический смыс:t-время,s(t)-закон прямолинейного движения,тоS`(t)=v(t) движение в момент времени t.
Если существует производная функции в этой точке,то функция в точке называется дифференцируемой в этой точке.
Теорема: Если функция y=f(x)дифференцируема в некоторой точке х,то она непрерывна в этой точке. Следствие:Если ф-я y=f(x) терпит разрыв в точке х,то производная в этой точке не существует.Необходимое условие существования производной: функция должна быть непрерывной.
Основные правила дифференцирования: производная от суммы и разности функций, производная от произведения и от дроби. Производная сложной и обратной функции.Основные правила дифференцирования: 1Производная от постоянной равна 0. 2Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: 3Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: 4Производная частного двух функций, если равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: Следствие: постоянный множитель можно выносить за знак производной: Производная от сложной функции: Если функция,где дифференцируемые функции, то производная будет равна производной внешней функции на производную внутренней функции: Производная от обратной функции: Если функция -дифференцируемая функция и существует обратная функция,то 22. Производная показательно-степенной функции. Логарифмическое дифференцирование. Дифференцирование параметрически заданных функций.
Логарифмическое дифференцирование:
Это дифференцирование функции с предварительным ее логарифмированием. Используется, если функция показательно-степенная или упрощается при логарифмировании.
1.Производная показательно-степенной функции:


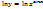




2. Логарифмирование:
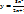

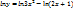

Дифференцирование параметрически заданных функций: 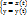

23. Касательная и нормаль к плоской кривой. Угол между прямыми.
Угол между кривыми -угол между касательными к кривым в точке пересечения.
Уравнение касательной: y-y0=f|(x0)*(x-x0)
Нормаль к кривой - прямая, перпендикулярная касательной в точке касания.
Уравнение нормали: 
24. Теоремы о дифференцируемых функциях: теоремы Ролля и Лангранжа. Формула конечных приращений.
Теорема Роля(теорема о нулях производной).
Пусть функция f(x) непрерывна на отрезке [a;b], дифференцируема во всех внутренних точках  и принимает на концах отрезка одинаковые значения f(a)=f(b),тогда существует по крайней мере одна точка
и принимает на концах отрезка одинаковые значения f(a)=f(b),тогда существует по крайней мере одна точка  в которой производная функции равна 0.
в которой производная функции равна 0.
Геометрический смысл: Если f(a)=f(b),то найдется хотя бы одна точка 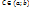 , в которой касательная параллельна оси ОХ
, в которой касательная параллельна оси ОХ
Если производная в т.М существует, то уравнение касательной имеет вид:
У|(М): y-y0=f|(x0)*(x-x0)
Км= 
Уравнение нормали: 
Теорема Лагранжа(теорема о конечных приращениях).
Если функция f(x) непрерывна на отрезке [a;b], дифференцируема во всех внутренних точках, то найдется хотя бы одна точка  для которой выполняется равенство:
для которой выполняется равенство: 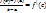
Геометрический смысл:На всякой дуге АВ графика дифференцируемой функции найдется точка,в которой касательная параллельна хорде.
Следствие(формула конечных приращений)
b-a=∆x,f(b)-f(a)=∆y, 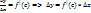 , где С- точка между х и х+∆х
, где С- точка между х и х+∆х 
Следствие(признак постоянства функции):
Если функция f(x) дифференцируема и на некотором промежутке ее производная равна 0,то функция является постоянной на этом промежутке.
25.Правило Лопиталя, его применение для раскрытия неопределенностей.
Правило: Предел отношения в двух бесконечно-малых или бесконечно-больших функциях при
х->а равен пределу отношения их производных, если предел отношения производных существует.
Правило Лопиталя помогает раскрыть неопределенности вида 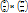
При помощи правила Лопиталя можно раскрывать и неопределенности вида(преобразовав их к виду 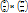 ):
):
 ,
,  ,
,  ,
, 
26.Монотонность функции на интервале. Достаточные условия возрастания(убывания) функции на интервале. Экстремумы функции. Необходимые условия существования экстремума дифференцируемой функции в точке.
Монотонность функции на интервале.
Пусть функция y=f(x) определена при  .
.
Функция y=f(x)называется возрастающей на интервале (a;b), если любому большему значению аргумента из этого интервала соответствует большее значение функции.
Функция называется y=f(x)называется убывающей на интервале (a;b), если любому большему значению аргумента из этого интервала соответствует наименьшее значение функции.
Достаточное условие монотонности функции на промежутке:
Если y=f(x) дифференцируемая функция на (a;b) и ее производная f|(x) сохраняет знак для любого Х из этого интервала, то функция f(x) сохраняется монотонность на этом промежутке, а именно:
f|(x)>0,  , то функция возрастает
, то функция возрастает
f|(x)<0,  , то функция убывает
, то функция убывает
Экстремумы функции.
Пусть х0- внутренняя точка области определения функции(ООФ).
Точка х0 называется точкой максимума функци и, если существует окрестность этой точки (UXо),такая что f(x0)> f(x) для 
|

 ,то х0-критическая точка.
,то х0-критическая точка. М u m могут достигаться либо в критических точках,либо на концах отрезка.
М u m могут достигаться либо в критических точках,либо на концах отрезка. ; l- график функции
; l- график функции , l-график функции.
, l-график функции.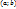 ,то график функции сохраняет выпуклость или вогнутость на этом промежутке, А именно:
,то график функции сохраняет выпуклость или вогнутость на этом промежутке, А именно: и х0 – критическая точка по 2 производной.
и х0 – критическая точка по 2 производной.


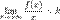
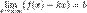
 ), то наклонной асимптоты при
), то наклонной асимптоты при 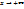 (или
(или  ) не существует!
) не существует!


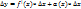
 и вычисляемая по формуле:
и вычисляемая по формуле:







Дата добавления: 2015-09-04; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Непрерывность функции в точке.Точки разрыва функции и их классификация.Свойства непрерывных функций.Свойства функций,непрерывных на отрезке. | | | РАСЧЕТ ТОКОВ КОРОТКОГО ЗАМЫКАНИЯ |