Определение 9.1

Пусть функция y=f(x), определена и непрерывна на промежутке [a,b], достигает на нем своего наибольшего (наименьшего) значения, если существует точка c, принадлежащая этому промежутку, такая, что для всех х из [a,b] выполняется неравенство

.

Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции y = f(x) на отрезке [a,b]:

1. Найти ;

2. Найти точки, в которых 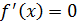или 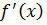не существует, и отобрать из них те, что лежат внутри отрезка [ a,b ];

3. Вычислить значения функции y=f(x) в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции y=f(x) на отрезке [ a,b ], которые можно обозначить так: .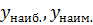

Если поставлена задача найти для непрерывной на (a,b) функции y=f(x), то она решается по тому же правилу, что соответствующая задача для отрезка [ a,b ].

Замечание: на третьем этапе вместо вычисления значений функции на концах отрезка находят пределы функции при приближении к концам интервала.

Иногда для отыскания наибольшего или наименьшего значения непрерывной функции y=f(x) на промежутке (a,b)полезны два утверждения:

1. Если функция y=f(x) имеет в промежутке Х только одну точку экстремума x=c, причем это точка максимума, то f(c) - наибольшее значение функции на промежутке Х;

2. Если функция y=f(x) имеет в промежутке Х только одну точку экстремума x=c, причем это точка минимума, то f(c) - наименьшее значение функции на промежутке Х.

Дата добавления: 2015-09-05