Читайте также:
|
Уравнение для дискретного аналога можно записать в виде
.
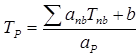Если в правую часть добавить и вычесть Т*Р, получим
.
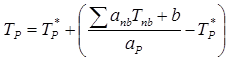где в круглых скобках содержится изменение ТР, полученное на текущей итерации. Это изменение можно скорректировать введением коэффициента релаксации a, при этом
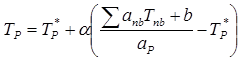(4.15)
или
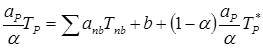
Во-первых, следует отметить, что при сходимости итераций ТР становится равным Т*Р и из уравнения (4.15) следует, что полученное в результате итераций значение ТР удовлетворяет исходному уравнению (4.3). При сходящемся процессе окончательное решение хотя и получается с помощью произвольного коэффициента релаксации или другими подобными способами, но должно удовлетворять исходному дискретному аналогу.
Когда коэффициент релаксации a в (4.15) изменяется от 0 до 1, имеем нижнюю релаксацию, при которой ТР остается близким к Т*Р. Для очень малых значений a изменение ТР становится очень медленным. В том случае, когда a>1, имеем верхнюю релаксацию.
Нет общих правил для выбора наилучшего значения a. Оптимальное значение зависит от целого ряда факторов, таких, как физическая основа задачи, число узловых точек, шаг сетки, используемый итерационный метод. Обычно подходящее значение a можно найти из предварительных расчетов данной задачи.
Нет необходимости в течение всего расчета сохранять одно и то же значение a. Это значение может изменяться от итерации к итерации. В действительности возможен (хотя это и не очень удобно) выбор различных значений a для каждой узловой точки.
Дата добавления: 2015-07-11; просмотров: 79 | Нарушение авторских прав