Метод переменных направлений (полинейный метод)

Построим удобную комбинацию прямого метода (TDMA) для одномерных задач и метода Гаусса - Зейделя. Выберем сеточную линию (линию, состоящую из узловых точек, например, в направлении оси у), предположим, что известны самые последние значения температуры на соседних сеточных линиях (т.е. на сеточных линиях, ближайших к узловым точкам на исходной сеточной линии вдоль осей х и z), и решим методом TDMA уравнения для температур в узловых точках вдоль выбранной линии.

Выполним эту процедуру для всех линий в одном направлении и повторим ее, если это необходимо, в другом направлении (или направлениях). Хотя метод можно применять к двух- и трехмерным задачам, для простоты рассмотрим только двухмерную задачу.

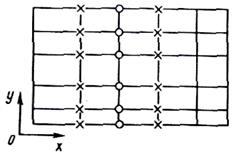Рис. 4.8 К методу переменных направлений (кружками обозначена выбранная линия)

Рассмотрим дискретный аналог для узловых точек вдоль выбранной линии. Он содержит температуры в точках (показанных крестиками на рис. 4.8) двух соседних линий. Если взять для этих температур самые последние (в итерационном смысле) значения, дискретный аналог для узлов (показанных кружками) вдоль выбранной линии будет выглядеть подобно одномерному дискретному аналогу и его можно решить с помощью метода TDMA.

Эта процедура выполняется для всех линий в направлении оси у и может быть аналогично выполнена для линий в направлении оси х.

Сходимость полинейного метода более быстрая, поскольку информация о граничных условиях с концов линии сразу передается во внутреннюю часть области независимо от того, сколько точек лежит на линии. Скорость передачи информации в поперечном направлении такая же, как и в поточечном методе.

С помощью перемены направлений, в которых TDMA применяется поперек, можно быстро передать информацию о граничных условиях внутрь области.

Часто геометрия и другие свойства задачи отражаются, например, в коэффициентах дискретного аналога для точек по направлению оси у, делая их намного больше, чем соответствующие коэффициенты в направлении оси х (рис. 4.9). В таком случае особенно быстрая сходимость получается, когда поперечный TDMA применяется в направлении оси у (направление больших коэффициентов). Вот почему предполагаемые значения температуры подставляются вместо значений температуры вдоль соседних линий, имеющих существенное влияние на дискретный аналог.

Рис. 4.9 Случай, в котором коэффициенты в направлении оси y намного больше коэффициентов в направлении оси x   Рис. 4.10 Граничные условия, для которых более удобен расчет слева направо (штриховкой изображена адиабатическая поверхность)

Так же как и выбор поперечного направления, в некоторых случаях важен выбор направления, вдоль которого производится последовательный переход от одной продольной линии к другой. Для ГУ, показанных на рис. 4.10, известное значение температуры будет передаваться внутрь области в направлении слева направо (выбираем левую границу области первой продольной линией и затем последовательно по линиям двигаемся направо). В то же время передача информации в направлении справа налево бесполезна, поскольку на правой границе неизвестно значение температуры (аналогично для поточечной схемы). Выбор направления перехода от одной продольной линии к другой особенно важен, когда рассматривается задача с конвекцией.

Очевидно, что выбор этого направления вверх по потоку будет обеспечивать более быструю сходимость, чем в противоположном случае.

Дата добавления: 2015-07-11