Дискретный аналог для трех измерений

Для построения трех мерной конфигурации добавим еще точки Т (Top - верх)и В (Bottom - низ) на оси z (см. рис. 4.7). Дискретный аналог имеет вид

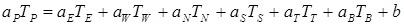, (4.11)

где ; ; ; ; ; ; ; ; .

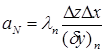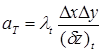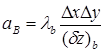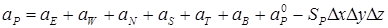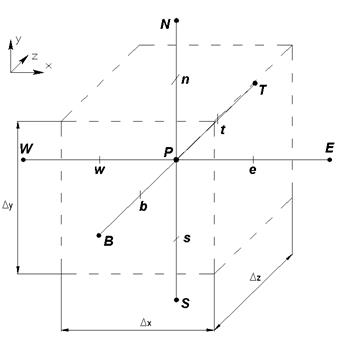
Рис. 4.6 Расположение точек для 3D дискретного аналога

Замечания:

1. Коэффициенты представляют собой проводимости, т.е. величины, обратные R между E … B и Р точками;
2. Член - внутренняя энергия (отнесенная к Δt), содержащаяся в КО в момент времени t;
3. b – сумма внутренней энергии и мощности тепловыделения в контрольном объеме;
4. Коэффициент а_р представляет собой сумму всех соседних коэффициентов (включая ) и вклад от линеаризованного источникового члена.

Дата добавления: 2015-07-11