Особенности дискретных аналогов не в ПДСК

До сих пор дискретные аналоги записывались с помощью сетки в прямоугольной декартовой системе координат. Далее почти везде будет употребляться та же система координат, поскольку она обеспечивает удобства записи и легкость понимания. Однако излагаемые методы не ограничены сетками в декартовой системе координат, их можно использовать для сеток в любой ортогональной системе координат. Для иллюстрации записи дискретного аналога в другой системе координат рассмотрим двухмерную задачу в полярной системе координат. Аналогом уравнения (4.9) в полярной системе координат является следующее уравнение:

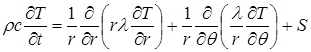(4.12)

Рис. 4.7 Сетка и КО в полярных координатах

Сетка и КО в координатах r и 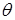показаны на рис. 4.7. Толщина КО в направлении оси z принимается равной единице. Для получения дискретного аналога умножим уравнение (4.12) на r и проинтегрируем соответственно по r и 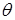в пределах КО (эта операция дает интеграл по объему, так как представляет собой элемент объема единичной толщины). После преобразований получим дискретный аналог для нестационарной двухмерной задачи теплопроводности в полярной системе координат

, (4.13)

где ; ; , ; , ; .

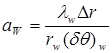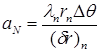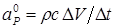Здесь (следует заметить, что может и не быть равным 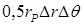, если Р не лежит посередине между n и s). Т.е. особенностью является только геометрия. Для неортогональных сеток необходима более сложная запись дискретного аналога.

Дата добавления: 2015-07-11