Обобщенный дискретный аналог

Что касается общего дифференциального уравнения для Ф, то теперь мы умеем в одномерном случае аппроксимировать диффузионный и источниковый члены. Обратимся к нестационарному члену и временно опустим источниковый член. Таким образом, ищем решение нестационарного одномерного уравнения теплопроводности

(4.4)

В дальнейшем для удобства будем полагать постоянным. Поскольку время является однонаправленной координатой, решение получаем, передвигаясь во времени от заданного начального распределения температуры. Таким образом, на типичном временном шаге по заданным значениям Т в узловых точках для времени t надо определить значения Т для времени t+Dt. Старые (заданные) значения Т в узловых точках обозначим T_P⁰, T_E⁰, T_W⁰, а новые (неизвестные) значения для времени t+Dt — T_P¹, T_E¹, T_W¹.

Дискретный аналог получим путем интегрирования уравнения (4.4) по контрольному объему и по временному интервалу от t до t+Dt. Таким образом,

,

где пределы интегрирования выбраны в соответствии с физическим смыслом членов. Для представления члена дT/дt предположим, что значение T в узловой точке распространено на весь КО, тогда

Следуя способу аппроксимации члена lдT/дt в стационарном случае, получаем

. (4.5)

На данном этапе необходимо ввести предположение относительно, изменения во времени от t до t+Dt температур Т_Р, Т_Е и T_W. Возможны различные предположения, и одно из них имеет следующий вид:

,

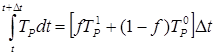где f — весовой коэффициент, изменяющийся от 0 до 1. Используя аналогичные соотношения для интегралов от Т_Е до T_W из уравнения (4.5), находим

Преобразуя это выражение, опустим индекс 1 и запомним, что Т_Р, Т_Е и T_W с этого момента будут означать новые значения T для времени t+Dt. В результате имеем (4.6)

,

где , , ,

Дата добавления: 2015-07-11