Критерий Скарбороу

Достаточным условием для сходимости метода Гаусса - Зейделя является

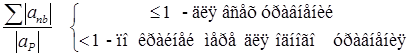(4.14)

Примечание:

1. Критерий является достаточным, но не необходимым условием. Это означает, что даже при нарушении соотношений (4.14) может иметь место сходимость.

2. Дискретные аналоги должны удовлетворять критерию Скарбороу для того, чтобы сходимость была гарантирована, по крайней мере, для одного итерационного метода.

3. Некоторые из основных правил, которые были мотивированы физическими соображениями, могут быть теперь рассмотрены сточки зрения удовлетворения критерия Скарбороу. Например, наличие отрицательного S_P приведет к строгому соблюдению неравенства (4.14). С учетом этого может также быть рассмотрено требование положительности коэффициентов. Если некоторые коэффициенты будут отрицательны, то а_Р (который обычно равняется ) может иметь значение меньшее, чем сумма модулей всех коэффициентов (так как ), что приведет к нарушению требований (4.14).

4. Если и все коэффициенты a_nb>0, то 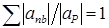для всех уравнений. Где же в таком случае уравнение, для которого значение это значение станет меньше единицы? Ответ заключается в граничных условиях. Для задачи, имеющей определенное решение, температура должна быть задана, по крайней мере, в одной граничной точке. Из уравнения дискретного аналога, в котором появляется эта точка, находим, что . Это происходит потому, что сумму a_nb, входящую в критерий Скарбороу, надо рассчитывать как сумму коэффициентов только в неизвестных соседних точках, а коэффициент a_P должен представлять сумму всех соседних коэффициентов, включая коэффициент в граничной точке.

Главным недостатком метода Гаусса - Зейделя является очень медленная сходимость, особенно когда используется большое число узловых точек. Причина медленной сходимости очевидна: метод передает информацию о граничных условиях со скоростью один сеточный интервал за итерацию.

Дата добавления: 2015-07-11