Явная, Кранка-Николсона и полностью неявная схемы

Для определенных конкретных значений весового коэффициента f дискретный аналог приводится к хорошо известным схемам для параболических дифференциальных уравнений. В частности, для f = 0 получаем явную схему, для f = 0,5 — схему Кранка — Николсона и для f = 1 — полностью неявную схему. Кратко рассмотрим эти схемы и покажем, что неявная схема наиболее предпочтительна. Различные значения f можно интерпретировать как характеристику изменения ТР от t, показанного на рис. 4.5. Явная схема. f = 0. По существу предполагает, что старое значение TP^0 существует в пределах всего временного шага, за исключением точки t+Dt.

Рис. 4.5 Изменение температуры по времени для явной схемы (1), схемы Кранка-Николсона (2) и полностью неявной схемы (3).

Для явной схемы уравнение (4.6) принимает следующий вид:

.

Это означает, что Т_Р не зависит от других неизвестных, таких, как Т_E или Т_W, а является явно определенной по известным температурам T_P⁰, T_E⁰, T_W⁰. Поэтому схема и называется явной. Любая схема с f ≠1 должна быть неявной, так как Т_Р зависит от неизвестных Т_E и Т_W,, в этом случае необходимо решать одновременно несколько уравнений. Удобство явной схемы в этом отношении компенсируется, однако, рядом ограничений. Анализируя (4.6) для явной схемы и вспоминая основное правило о положительных коэффициентах (правило 2), замечаем, что коэффициент при T_P⁰ может принимать отрицательные значения (значение T_P⁰ рассматривается как соседнее с Т_Р по временной координате).

Действительно, для того чтобы этот коэффициент был положительным, шаг по времени должен быть достаточно малым, т.е. a_P>a_E+a_W. Для постоянного коэффициента теплопроводности и Dx=(дx)e=(дx)w это условие запишется в виде

(4.7)

Если это условие нарушается, то могут возникнуть физически неправдоподобные результаты, так как из отрицательности коэффициента следует, что увеличение T_P⁰ приводит к уменьшению Т_Р. Уравнение (4.7) является хорошо известным критерием устойчивости явной схемы.

Схема Кранка-Николсона. f = 0.5. Схема предполагает линейное изменение Т_Р. С первого взгляда линейное изменение должно быть более разумным, чем две другие альтернативы. Обычно схема Кранка-Николсона считается безусловно устойчивой. Иногда это объясняют исходя из того, что физически реальное решение будет получаться независимо от значения шага по времени. Однако в этом случае могут иметь место колеблющиеся решения. Устойчивость в математическом смысле просто гарантирует, что эти колебания будут, в конечном счете, затухать, но это не обеспечивает физически правдоподобного решения.

В рамках нашей модели такое поведение легко объясняется. Для f = 0.5 коэффициент при T_P⁰ в уравнении (4.6) становится равным a_P⁰-(a_E+a_W)/2. Для постоянного коэффициента теплопроводности и равномерной сетки этот коэффициент, как видно, равен . Когда шаг по времени недостаточно мал, этот коэффициент может становиться отрицательным, что делает возможным физически неправдоподобный результат.

Неявная схема. f = 1. Предполагает, что в момент t Т_Р резко изменяется от T_P⁰ до T_P¹, а затем остается равной T_P¹ на всем временном, шаге и температура в пределах временного шага характеризуется новым значением Т_Р.

Если потребовать, чтобы коэффициент при T_P⁰ в уравнении (4.6) не был отрицательным, то только постоянная величина f = 1 обеспечит это условие (конечно, это не имеет смысла для f >1). Таким образом, полностью неявная схема (f = 1) удовлетворяет требованиям простоты и физически обоснованного поведения.

Запишем уравнение (4.6) в полностью неявном виде. Для этого введем линеаризованный источниковый член, который примем уменьшающимся во времени. В результате получим

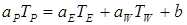, (4.8)

где , , , , .

Видно, что при это уравнение приводится к стационарному дискретному аналогу. Основным принципом полностью неявной схемы является то, что в пределах всего шага по времени температура принимается равной новому значению Т_Р. Таким образом, если коэффициент теплопроводности l_Р зависит от температуры, он должен пересчитываться через Т_Р в итерационном процессе точно так же как. и при решении стационарной задачи.

В STAR-CD используется неявная схема.

Дата добавления: 2015-07-11