Поточечный последовательный метод Гаусса - Зейделя

Простейшим из всех итерационных методов является метод Гаусса - Зейделя, в котором значения переменной рассчитываются путем обращения в определенном порядке к каждой узловой точке. В оперативной памяти держится только один массив значений Т. По мере обращения к очередной узловой точке соответствующее значение Т в оперативной памяти (начальное приближение или значение Т с предыдущей итерации) заменяется на новое. Если дискретный аналог записан в виде (4.3)

,

где индекс nb обозначает соседнюю точку, то новое значение T_P в рассматриваемой узловой точке рассчитывается по соотношению

где T^*_nb - это самое последнее значение температуры в соседних точках, которое находится в оперативной памяти. Для соседних точек, к которым уже обращались в ходе текущей итерации, T^*_nb является новым рассчитанным значением, а для остальных соседних точек T^*_nb - значение с предыдущей итерации. Когда все узловые точки рассмотрены подобным образом, одна итерация метода Гаусса - Зейделя закончена.

Для иллюстрации метода рассмотрим два очень простых примера.

Пример. Уравнения 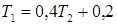и . Решение

№ итерации							…	∞
T1		0,2	0,68	0,872	0,949	0,98	…	1,0
T2		1,2	1,68	1,872	1,949	1,98	…	2,0

Как видно из примера, можно получить точное решение уравнений, начиная с некоторых произвольных значений. Интересной особенностью итерационных методов является то, что точность расчета может быть не очень высокой на промежуточных этапах. Приближенность расчетов и даже погрешности уничтожаются в том случае, когда промежуточные значения используются просто как приближения для последующих итераций. Рассмотрим следующий пример.

Пример. Уравнения 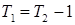и . Решение

№ итерации
T1		-1	-4	-11,5	-30,25
T2		-3	-10,5	-29,25	-76,13

Здесь итерационный процесс расходится. Однако эти уравнения представляют собой просто вариант предыдущих уравнений, для которых получен сходящийся итерационный процесс. Таким образом, делаем вывод, что метод Гаусса - Зейделя не всегда является сходящимся.

Дата добавления: 2015-07-11